Question

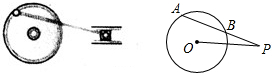
某机械传动装置如图所示，⊙O的半径R=6cm，点A在⊙O上运动．某一时刻，连杆PA交⊙O于点B，现测得PA=18cm，PB=8cm．
（1）求点O到AB的距离；
（2）连接OP，求sinP的值．

Answer 1

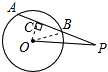解：∵PA=18，PB=8
∴AB=10
作OC⊥AB于C，连接OB，
∴BC=5，OB=6．
∴OC=；

（2）CP=13，OC=
OP=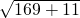=6，
∴sinP=．
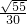分析：（1）连接PO，欲求PO的长可延长PO，通过构建割线，运用割线定理求解．
（2）用勾股定理求得OP的长，然后正弦的定义求解即可．
点评：本题考查了垂径定理的知识，解题的关键是正确地构造直角三角形．