题目内容
(2010•漳州)李老师为了了解九(上)期末考数学试卷中选择题的得分情况,对她所任教的九(1)班和九(2)班的学生试卷中选择题的得分情况进行抽查.下图表示的是从以上两个班级中各随机抽取的10名学生的得分情况.(注:每份试卷的选择题共10小题,每小题3分,共计30分.)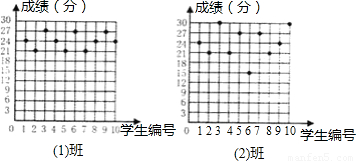
(1)利用上图提供的信息,补全下表:
| 各班所抽查学生成绩 | 平均数(分) | 中位数(分) | 众数(分) |
| (1)班抽查的10名学生成绩 | ①______ | 24 | 24 |
| (2)班抽查的10名学生成绩 | 24 | ②______ | ③______ |
(3)若规定24分以上(含24分)为“优秀”,李老师所任教的两个班级各有学生60名,请估计两班各有多少名学生的成绩达到“优秀”?
【答案】分析:(1)根据平均数、中位数和众数的概念直接求解,补全图形;
(2)观察图形,根据数据波动的大小可判断;
(3)用总人数乘以优秀率就可得出各班达到优秀人数.
解答:解:(1)九(1)数据为:24,21,27,24,21,27,21,24,27,24,
∴九(1)平均分=(24+21+27+24+21+27+21+24+27+24)÷10=24(分);
九(2)数据为:24,21,30,21,27,15,27,21,24,30,
∴九(2)中位数=(24+24)÷2=24(分),众数为21(分);则可补充下图:
;
(2)观察图形可知,九(1)班的数据波动较小,所以它的方差小,学生整体成绩较稳定;
故填九(1).
(3)九(1)班的优秀人数:60×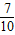 =42,
=42,
九(2)的优秀人数:60× =36.
=36.
即估计九(1)班有42名学生达到优秀,九(2)班有36名学生达到优秀.
点评:本题考查了平均数、中位数、众数和方差的意义.平均数平均数表示一组数据的平均程度;中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数);众数是一组数据中出现次数最多的数据;方差是用来衡量一组数据波动大小的量.
(2)观察图形,根据数据波动的大小可判断;
(3)用总人数乘以优秀率就可得出各班达到优秀人数.
解答:解:(1)九(1)数据为:24,21,27,24,21,27,21,24,27,24,
∴九(1)平均分=(24+21+27+24+21+27+21+24+27+24)÷10=24(分);
九(2)数据为:24,21,30,21,27,15,27,21,24,30,
∴九(2)中位数=(24+24)÷2=24(分),众数为21(分);则可补充下图:
| 各班所抽查学生成绩 | 平均数(分) | 中位数(分) | 众数(分) |
| (1)班抽查的10名学生成绩 | ①24 | 24 | 24 |
| (2)班抽查的10名学生成绩 | 24 | ②24 | ③21 |
(2)观察图形可知,九(1)班的数据波动较小,所以它的方差小,学生整体成绩较稳定;
故填九(1).
(3)九(1)班的优秀人数:60×
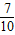 =42,
=42,九(2)的优秀人数:60×
 =36.
=36.即估计九(1)班有42名学生达到优秀,九(2)班有36名学生达到优秀.
点评:本题考查了平均数、中位数、众数和方差的意义.平均数平均数表示一组数据的平均程度;中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数);众数是一组数据中出现次数最多的数据;方差是用来衡量一组数据波动大小的量.

练习册系列答案
相关题目
(2010•漳州)李老师为了了解九(上)期末考数学试卷中选择题的得分情况,对她所任教的九(1)班和九(2)班的学生试卷中选择题的得分情况进行抽查.下图表示的是从以上两个班级中各随机抽取的10名学生的得分情况.(注:每份试卷的选择题共10小题,每小题3分,共计30分.)

(1)利用上图提供的信息,补全下表:
(2)观察上图点的分布情况,你认为______班学生整体成绩较稳定;
(3)若规定24分以上(含24分)为“优秀”,李老师所任教的两个班级各有学生60名,请估计两班各有多少名学生的成绩达到“优秀”?

(1)利用上图提供的信息,补全下表:
| 各班所抽查学生成绩 | 平均数(分) | 中位数(分) | 众数(分) |
| (1)班抽查的10名学生成绩 | ①______ | 24 | 24 |
| (2)班抽查的10名学生成绩 | 24 | ②______ | ③______ |
(3)若规定24分以上(含24分)为“优秀”,李老师所任教的两个班级各有学生60名,请估计两班各有多少名学生的成绩达到“优秀”?
(2010•漳州)李老师为了了解九(上)期末考数学试卷中选择题的得分情况,对她所任教的九(1)班和九(2)班的学生试卷中选择题的得分情况进行抽查.下图表示的是从以上两个班级中各随机抽取的10名学生的得分情况.(注:每份试卷的选择题共10小题,每小题3分,共计30分.)

(1)利用上图提供的信息,补全下表:
(2)观察上图点的分布情况,你认为______班学生整体成绩较稳定;
(3)若规定24分以上(含24分)为“优秀”,李老师所任教的两个班级各有学生60名,请估计两班各有多少名学生的成绩达到“优秀”?

(1)利用上图提供的信息,补全下表:
| 各班所抽查学生成绩 | 平均数(分) | 中位数(分) | 众数(分) |
| (1)班抽查的10名学生成绩 | ①______ | 24 | 24 |
| (2)班抽查的10名学生成绩 | 24 | ②______ | ③______ |
(3)若规定24分以上(含24分)为“优秀”,李老师所任教的两个班级各有学生60名,请估计两班各有多少名学生的成绩达到“优秀”?