Question

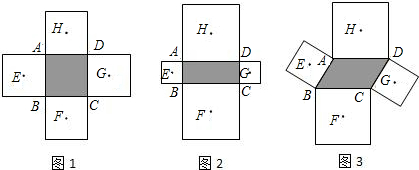
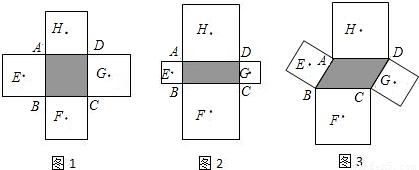
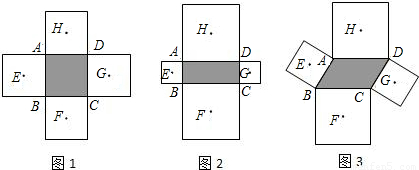
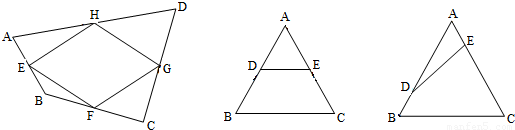
如图1，若顺次连接四边形ABCD各边中点所得四边形EFGH是菱形，则称原四边形ABCD为“中母菱形”．定义：若四边形的对角线相等，那么这个四边形是中母菱形．
（1）请写一个你学过的特殊四边形中是中母菱形的图形的名称．
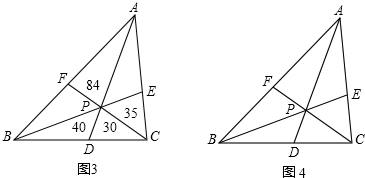
（2）如图有等边三角形ABC中，D、E分别是AB、AC的中点，连接DE，猜想图中哪个四边形是中母菱形，并加以证明．
（3）在等边三角形ABC中，若D、E不是AB、AC的中点，且BD=AE，探究满足上述条件的图形中是否在中母菱形，并证明你的结论．

Answer 1

【答案】分析：（1）从学过的特殊图形中，寻找对角线相等的图形（正方形、矩形、等腰梯形等）；
（2）欲证明四边形DBCE是中母菱形，只需证明该四边形的对角线DC=BE即可；
（3）通过全等三角形的判定定理SAS证得△ABE≌△BCD，然后根据全等三角形的对应边相等的性质推知四边形DBCE的对角线BE=DC，所以四边形DBCE是中母菱形．
解答：解：（1）矩形；等腰梯形．

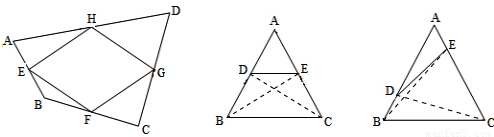
（2）四边形DBCE是中母菱形．
证明：连接DC、BE．
∵D、E分别是AB、AC的中点，
∴DE平行BC，DE=BC，
∴四边形DBCE是梯形．
又∵AB=AC，D、E分别是AB、AC的中点，
∴DB=EC，
∴梯形DBCE是等腰梯形．
∴DC=BE，
∴四边形DBCE是中母菱形．

（3）四边形DBCE是中母菱形．
证明：连接DC、BE．
∵BD=AE，∠BAE=∠CBD，AB=BC
∴△ABE≌△BCD
∴BE=DC
∴四边形DBEC是中母菱形．
点评：本题主要考查了全等三角形的判定与性质、菱形是性质、等边三角形的性质以及三角形中位线定理．解答本题的主要依据是中母菱形的定义的定义：若四边形的对角线相等，那么这个四边形是中母菱形．