题目内容
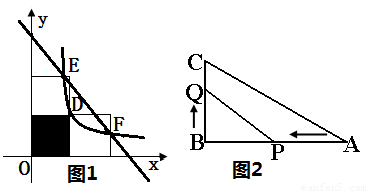
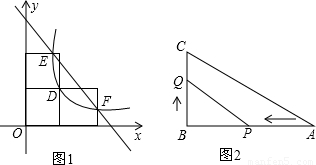
如图1是三个边长为2的正方形小方格,反比例函数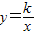 经过正方形格点D,与小方格交于点E、点F,直线EF的解析式为y=mx+a.如图2所示的△ABC为Rt△,∠B=90°,AB=10厘米,BC=a厘米.
经过正方形格点D,与小方格交于点E、点F,直线EF的解析式为y=mx+a.如图2所示的△ABC为Rt△,∠B=90°,AB=10厘米,BC=a厘米.(1)求反比例函数的解析式.
(2)求一次函数的解析式.
(3)已知点P从点A出发沿AB边向点B以1厘米/秒的速度移动,点Q从点B出发沿BC边向点C以2厘米/秒的速度移动,如果P、Q两点同时出发,几秒种后,△BPQ的面积与是△ABC的面积一半?
【答案】分析:(1)根据已知得出D点坐标为:(2,2),即可求出反比例函数解析式;
(2)根据E,F点坐标特点以及(1)中函数解析式,即可得出E,F点坐标,求出解析式即可;
(3)根据Q,P运动速度与方向以及得出BP=10-t,BQ=2t,以及S△BPQ= (10-t)×2t,再利用△BPQ的面积与是△ABC的面积一半求出即可.
(10-t)×2t,再利用△BPQ的面积与是△ABC的面积一半求出即可.
解答:解:(1)∵如图1是三个边长为2的正方形小方格,
∴D点坐标为:(2,2),
∵反比例函数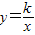 经过正方形格点D,
经过正方形格点D,
∴xy=k=4,
∴y= ,
,
(2)∵如图1是三个边长为2的正方形小方格,反比例函数 经过正方形格点D,与小方格交于点E、点F,
经过正方形格点D,与小方格交于点E、点F,
∴E点坐标为:(1,4),F点坐标为:(4,1),
∴ ,
,
解得: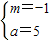 ,
,
∴一次函数的解析式为:y=-x+5;
(3)∵点P从点A出发沿AB边向点B以1厘米/秒的速度移动,点Q从点B出发沿BC边向点C以2厘米/秒的速度移动,
∴假设t秒后,△BPQ的面积与是△ABC的面积一半,
∴BP=10-t,BQ=2t,由(2)得出a=5,
∴S△BPQ= (10-t)×2t=-t2+10t,
(10-t)×2t=-t2+10t,
S△ABC= ×10×5=25,
×10×5=25,
∴25=2(-t2+10t),
∴2t2-20t+25=0,
解得:t=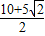 (不合题意舍去),或t=
(不合题意舍去),或t=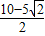 ,
,
∴P、Q两点同时出发, 秒种后,△BPQ的面积与是△ABC的面积一半.
秒种后,△BPQ的面积与是△ABC的面积一半.
点评:此题考查了待定系数法求一次函数解析式与反比例函数解析式以及一元二次方程中动点问题,正确求出E,F点坐标试求出一次函数解析式是解题关键.
(2)根据E,F点坐标特点以及(1)中函数解析式,即可得出E,F点坐标,求出解析式即可;
(3)根据Q,P运动速度与方向以及得出BP=10-t,BQ=2t,以及S△BPQ=
 (10-t)×2t,再利用△BPQ的面积与是△ABC的面积一半求出即可.
(10-t)×2t,再利用△BPQ的面积与是△ABC的面积一半求出即可.解答:解:(1)∵如图1是三个边长为2的正方形小方格,
∴D点坐标为:(2,2),
∵反比例函数
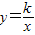 经过正方形格点D,
经过正方形格点D,∴xy=k=4,
∴y=
 ,
,(2)∵如图1是三个边长为2的正方形小方格,反比例函数
 经过正方形格点D,与小方格交于点E、点F,
经过正方形格点D,与小方格交于点E、点F,∴E点坐标为:(1,4),F点坐标为:(4,1),
∴
 ,
,解得:
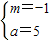 ,
,∴一次函数的解析式为:y=-x+5;
(3)∵点P从点A出发沿AB边向点B以1厘米/秒的速度移动,点Q从点B出发沿BC边向点C以2厘米/秒的速度移动,
∴假设t秒后,△BPQ的面积与是△ABC的面积一半,
∴BP=10-t,BQ=2t,由(2)得出a=5,
∴S△BPQ=
 (10-t)×2t=-t2+10t,
(10-t)×2t=-t2+10t,S△ABC=
 ×10×5=25,
×10×5=25,∴25=2(-t2+10t),
∴2t2-20t+25=0,
解得:t=
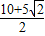 (不合题意舍去),或t=
(不合题意舍去),或t=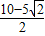 ,
,∴P、Q两点同时出发,
 秒种后,△BPQ的面积与是△ABC的面积一半.
秒种后,△BPQ的面积与是△ABC的面积一半.点评:此题考查了待定系数法求一次函数解析式与反比例函数解析式以及一元二次方程中动点问题,正确求出E,F点坐标试求出一次函数解析式是解题关键.

练习册系列答案
相关题目

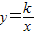 经过正方形格点D,与小方格交于点E、点F,直线EF的解析式为y=mx+a.如图2所示的△ABC为Rt△,∠B=90°,AB=10厘米,BC=a厘米.
经过正方形格点D,与小方格交于点E、点F,直线EF的解析式为y=mx+a.如图2所示的△ABC为Rt△,∠B=90°,AB=10厘米,BC=a厘米.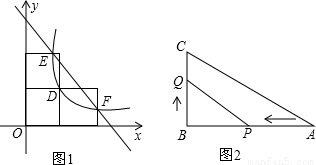
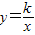 经过正方形格点D,与小方格交于点E、点F,直线EF的解析式为y=mx+a.如图2所示的△ABC为Rt△,∠B=90°,AB=10厘米,BC=a厘米.
经过正方形格点D,与小方格交于点E、点F,直线EF的解析式为y=mx+a.如图2所示的△ABC为Rt△,∠B=90°,AB=10厘米,BC=a厘米.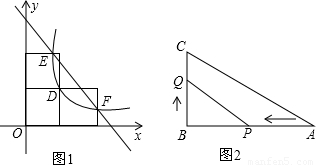
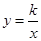 经过正方形
经过正方形