题目内容
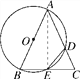
【题目】(2016·宁夏中考)如图,已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC.
(1)求证:AB=AC;
(2)若AB=4,BC=2![]() ,求CD的长.
,求CD的长.

【答案】(1)见解析 (2)CD=![]()
(1)证明:∵ED=EC,∴∠EDC=∠C.∵∠B+∠ADE=180°,∠EDC+∠ADE=180°,∴∠B=∠EDC,∴∠B=∠C,∴AB=AC;
(2)解:连接AE.∵AB为直径,∴AE⊥BC.由(1)知AB=AC,∴AC=4,BE=CE=![]() BC=
BC=![]() .∵∠C=∠C,∠EDC=∠B,∴△EDC∽△ABC,∴
.∵∠C=∠C,∠EDC=∠B,∴△EDC∽△ABC,∴![]() =
=![]() ,即CE·BC=CD·AC,∴
,即CE·BC=CD·AC,∴![]() ·2
·2![]() =4CD,∴CD=
=4CD,∴CD=![]() .
.
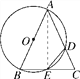
【解析】试题分析:(1)由等腰三角形的性质得到∠EDC=∠C,由圆内接四边形的性质得到∠EDC=∠B,由此推得∠B=∠C,由等腰三角形的判定即可证得结论;
(2)连接AE,由AB为直径,可证得AE⊥BC,由(1)知AB=AC,根据等腰三角形的“三线合一”求出CE的长,然后根据两角相等的三角形全等证明△EDC∽△ABC后即可求得CD的长.
试题解析:(1)证明:∵ED=EC,
∴∠EDC=∠C.
∵∠B+∠ADE=180°,∠EDC+∠ADE=180°,
∴∠B=∠EDC,
∴∠B=∠C,
∴AB=AC;
(2)解:连接AE.
∵AB为直径,
∴AE⊥BC.
由(1)知AB=AC,
∴AC=4,BE=CE=![]() BC=
BC=![]() .
.
∵∠C=∠C,∠EDC=∠B,
∴△EDC∽△ABC,
∴![]() =
=![]() ,
,
即CE·BC=CD·AC,
∴![]() ·2
·2![]() =4CD,
=4CD,
∴CD=![]() .
.

练习册系列答案
相关题目

