题目内容
 (注:本题分A、B两类题,大家可选做,两题都做已A类计分.)
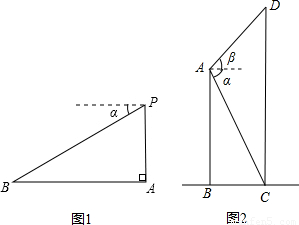
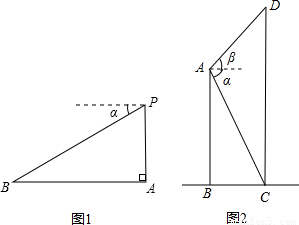
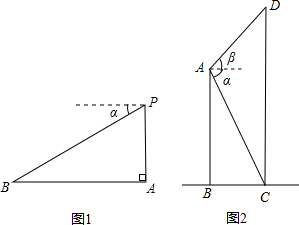
(注:本题分A、B两类题,大家可选做,两题都做已A类计分.)(A类)如图1,飞机P在目标A的正上方1100m处,飞行员测得地面目标B的俯角α=30°,求地面目标A、B之间的距离;(结果保留根号)
(B类)如图2,两建筑物AB、CD的水平距离BC=30 m,从点A测得点C的俯角α=60°,测得点D的仰角β=45°,求两建筑物AB、CD的高.(结果保留根号)
我选做的是
分析:A:在直角三角形中知道已知角和对边,求邻边,用正切计算即可.
B:在构建直角三角形后,利用60°、45°角的正切值,分别求出它们的对边,然后相加即可解答.
B:在构建直角三角形后,利用60°、45°角的正切值,分别求出它们的对边,然后相加即可解答.
解答: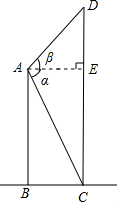 解:(A类)在Rt△PAB中,因为∠B=30°,
解:(A类)在Rt△PAB中,因为∠B=30°,
PA=1100m.
所以AB=PAcot30°=1100
(m).
答:A、B之间的距离为1100
m.
(B类)如图,过点A作AE⊥CD于E,则AE=BC=30m.
在Rt△ABC中,因为∠ACB=α=60°,BC=30m,
所以AB=BCtan60°=30
(m).
在Rt△ADE中,
因为β=45°,AE=30m,
所以DE=AE=30(m).
所以CD=DE+AB=30
+30(m).
答:两建筑物AB、CD的高分别为30
m、(30
+30)m.
 解:(A类)在Rt△PAB中,因为∠B=30°,
解:(A类)在Rt△PAB中,因为∠B=30°,PA=1100m.
所以AB=PAcot30°=1100
| 3 |
答:A、B之间的距离为1100
| 3 |
(B类)如图,过点A作AE⊥CD于E,则AE=BC=30m.
在Rt△ABC中,因为∠ACB=α=60°,BC=30m,
所以AB=BCtan60°=30
| 3 |
在Rt△ADE中,
因为β=45°,AE=30m,
所以DE=AE=30(m).
所以CD=DE+AB=30
| 3 |
答:两建筑物AB、CD的高分别为30
| 3 |
| 3 |
点评:本题要求学生借助仰角、俯角关系构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案
相关题目