题目内容
已知关于的方程 与
与 都有实数根,若这两个方程有且只有一个公共根,且
都有实数根,若这两个方程有且只有一个公共根,且 ,则称它们互为“同根轮换方程”.如
,则称它们互为“同根轮换方程”.如 与
与 互为“同根轮换方程”.
互为“同根轮换方程”.
(1)若关于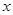 的方程
的方程 与
与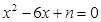 互为“同根轮换方程”,求
互为“同根轮换方程”,求 的值;
的值;
(2)若 是关于
是关于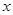 的方程
的方程 的实数根,
的实数根, 是关于
是关于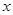 的方程
的方程 的实数根,当
的实数根,当 .
. 分别取何值时,方程
分别取何值时,方程 与
与 互为“同根轮换方程”,请说明理由.
互为“同根轮换方程”,请说明理由.
 与
与 都有实数根,若这两个方程有且只有一个公共根,且
都有实数根,若这两个方程有且只有一个公共根,且 ,则称它们互为“同根轮换方程”.如
,则称它们互为“同根轮换方程”.如 与
与 互为“同根轮换方程”.
互为“同根轮换方程”.(1)若关于
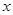 的方程
的方程 与
与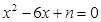 互为“同根轮换方程”,求
互为“同根轮换方程”,求 的值;
的值;(2)若
 是关于
是关于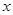 的方程
的方程 的实数根,
的实数根, 是关于
是关于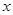 的方程
的方程 的实数根,当
的实数根,当 .
. 分别取何值时,方程
分别取何值时,方程 与
与 互为“同根轮换方程”,请说明理由.
互为“同根轮换方程”,请说明理由.(1)m=-12;(2)当p=q=-3a时,方程 与
与 互为“同根轮换方程”.
互为“同根轮换方程”.
 与
与 互为“同根轮换方程”.
互为“同根轮换方程”.试题分析:(1)根据同根方程条件:两个方程有且只有一个公共根,且
 ,先求出公共根,进而求出
,先求出公共根,进而求出 的值;
的值;(2)仿照(1)的过程求出
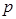 .
. 的取值,只要得到p=q,2a×
的取值,只要得到p=q,2a×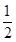 b=ab,即可判断方程
b=ab,即可判断方程 与
与 互为“同根轮换方程”.
互为“同根轮换方程”.试题解析:(1)∵方程x2+4x+m=0与x2-6x+n=0互为“同根轮换方程”,
∴4m=-6n.
设t是公共根,则有t2+4t+m=0,t2-6t+n=0.
解得,t=
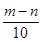 .
. ∵4m=-6n.
∴t=
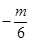 .
.∴(
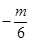 )2+4(
)2+4(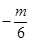 )+m=0.
)+m=0.∴m=-12.
(2)若方程x2+ax+b=0(b≠0)与
 有公共根.
有公共根.则由x2+ax+b=0,
 解得x=
解得x= .
. ∴
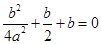 .
.∴b=-6a2.
当b=-6a2时,有x2+ax-6a2=0,x2+2ax-3a2=0.
解得,x1=-3a,x2=2a;x3=-3a,x4=a.
若p=q=-3a,
∵b≠0,∴-6a2≠0,∴a≠0.
∴2a≠a.即x2≠x4.
∵2a×
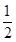 b=ab,
b=ab, ∴方程x2+ax+b=0(b≠0)与
 =0互为“同根轮换方程” .
=0互为“同根轮换方程” .
练习册系列答案
相关题目
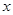 的方程
的方程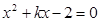
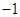 ,求另一个根及
,求另一个根及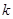 值.
值. ﹣
﹣ +1
+1 ,根据市场需要,今年该农场扩大了种植面积,并且全部种植了高产的新品种西瓜,已知西瓜的种植面积的增长率是亩产量的增长率的2倍,今年西瓜的总产量为
,根据市场需要,今年该农场扩大了种植面积,并且全部种植了高产的新品种西瓜,已知西瓜的种植面积的增长率是亩产量的增长率的2倍,今年西瓜的总产量为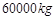 ,求西瓜亩产量的增长率.
,求西瓜亩产量的增长率. 的根是( )
的根是( )