题目内容
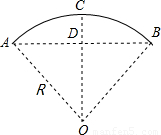
如图为某桥的桥拱平面图形，拱宽AB=12，拱高CD为4，则该桥拱所在圆弧的半径为
- A.4.5
- B.5.5
- C.6.5
- D.7.5
C
分析：根据垂径定理求出AD，在Rt△ADO中，根据勾股定理得出关于R的方程，求出方程的解即可．
解答：∵OC⊥AB，OC过O，
∴根据垂径定理得：AD=BD=6，
∵在Rt△ADO中，AD2+OD2=AO2，
∴62+（R-4）2=R2，
解得：R=6.5，
故选C．
点评：本题考查了勾股定理和垂径定理的应用，关键是构造直角三角形得出关于R的方程，题目比较典型，是一道比较好的题目．
分析：根据垂径定理求出AD，在Rt△ADO中，根据勾股定理得出关于R的方程，求出方程的解即可．
解答：∵OC⊥AB，OC过O，
∴根据垂径定理得：AD=BD=6，
∵在Rt△ADO中，AD2+OD2=AO2，
∴62+（R-4）2=R2，
解得：R=6.5，
故选C．
点评：本题考查了勾股定理和垂径定理的应用，关键是构造直角三角形得出关于R的方程，题目比较典型，是一道比较好的题目．
练习册系列答案
口算与应用题卡系列答案
名师点睛字词句段篇系列答案
相关题目
如图为某桥的桥拱平面图形，拱宽AB=12，拱高CD为4，则该桥拱所在圆弧的半径为（ ）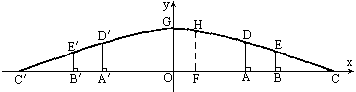
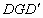部分为一段抛物线，顶点G的高度为8米，AD和
是两侧高为5.5米的支柱，OA和
为两个方向的汽车通行区，宽都为15米，线段CD和
为两段对称的上桥斜坡，其坡度为1∶4．
所在抛物线的解析式及
的长．
为支撑斜坡的立柱，其高都为4米，相应的AB和
为两个方向的行人及非机动车通行区，试求AB和
的宽．
)区域安全通过？请说明理由．
部分为一段抛物线，顶点G的高度为8米，AD和
是两侧高为5.5米的支柱，OA和
为两个方向的汽车通行区，宽都为15米，线段CD和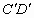
为两段对称的上桥斜坡，其坡度1：4.
所在抛物线的关系式及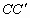
的长；
为支撑斜坡的立柱，其高都为4米，相应的AB和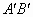
为两个方向的行人及非机动车通行区，试求AB和
的宽；
)区域安全通过？请说明理由.
