题目内容
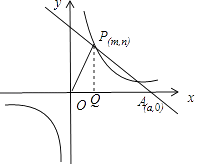
【题目】已知:O是坐标原点,P(m,n)(m>0)是函数y= ![]() (k>0)上的点,过点P作直线PA⊥OP于P,直线PA与x轴的正半轴交于点A(a,0)(a>m).设△OPA的面积为s,且s=1+
(k>0)上的点,过点P作直线PA⊥OP于P,直线PA与x轴的正半轴交于点A(a,0)(a>m).设△OPA的面积为s,且s=1+ ![]() .
.
(1)当n=1时,求点A的坐标;
(2)若OP=AP,求k的值;
(3)设n是小于20的整数,且k≠ ![]() ,求OP2的最小值.
,求OP2的最小值.
【答案】
(1)解:过点P作PQ⊥x轴于Q,则PQ=n,OQ=m,
当n=1时,s= ![]() ,
,
∴a= ![]() =
= ![]() .
.
(2)解:解法一:∵OP=AP,PA⊥OP,
∴△OPA是等腰直角三角形.
∴m=n= ![]() .
.
∴1+ ![]() =
= ![]() an.
an.
即n4﹣4n2+4=0,
∴k2﹣4k+4=0,
∴k=2.
解法二:∵OP=AP,PA⊥OP,
∴△OPA是等腰直角三角形.
∴m=n.
设△OPQ的面积为s1
则:s1= ![]() ∴
∴ ![]() mn=
mn= ![]() (1+
(1+ ![]() ),
),
即:n4﹣4n2+4=0,
∴k2﹣4k+4=0,
∴k=2.
(3)解:解法一:∵PA⊥OP,PQ⊥OA,
∴△OPQ∽△OAP.
设:△OPQ的面积为s1,则 ![]() =
= ![]()
即: ![]() =
= ![]() 化简得:
化简得:
化简得:
2n4+2k2﹣kn4﹣4k=0
(k﹣2)(2k﹣n4)=0,
∴k=2或k= ![]() (舍去),
(舍去),
∴当n是小于20的整数时,k=2.
∵OP2=n2+m2=n2+ ![]() 又m>0,k=2,
又m>0,k=2,
∴n是大于0且小于20的整数.
当n=1时,OP2=5,
当n=2时,OP2=5,
当n=3时,OP2=32+ ![]() =9+
=9+ ![]() =
= ![]() ,
,
当n是大于3且小于20的整数时,
即当n=4、5、6…19时,OP2的值分别是:
42+ ![]() 、52+
、52+ ![]() 、62+
、62+ ![]() …192+
…192+ ![]() ,
,
∵192+ ![]() >182+
>182+ ![]() >32+
>32+ ![]() >5,
>5,
∴OP2的最小值是5.
【解析】(1)利用△OPA面积定义构建关于a的方程,求出A的坐标;(2)由已知OP=AP,PA⊥OP,可得△OPA是等腰直角三角形, 由其面积构建关于n的方程,转化为k的方程,求出k;(3)利用相似三角形的面积比等于相似比的平方构建关于k的方程,最值问题的基本解决方法就是函数思想,利用勾股定理用m、n的代数式表达OP2,,在n的范围内求出OP2的最值.

【题目】抗震救灾中,某县粮食局为了保证库存粮食的安全,决定将甲、乙两个仓库的粮食,全部转移到具有较强抗震功能的A、B两仓库.已知甲库有粮食100吨,乙库有粮食80吨,而A库的容量为70吨,B库的容量为110吨.从甲、乙两库到A、B两库的路程和运费如下表:(表中“元/吨千米”表示每吨粮食运送1千米所需人民币)
路程(千米) | 运费(元/吨千米) | |||
甲库 | 乙库 | 甲库 | 乙库 | |
A库 | 20 | 15 | 12 | 12 |
B库 | 25 | 20 | 10 | 8 |
(1)若甲库运往A库粮食x吨,请写出将粮食运往A、B两库的总运费y(元)与x(吨)的函数关系式;
(2)当甲、乙两库各运往A、B两库多少吨粮食时,总运费最省,最省的总运费是多少?
【题目】某市举行知识大赛,A校、B校各派出5名选手组成代表队参加决赛,两校派出选手的决赛成绩如图所示.
(1)根据图示填写下表:
平均数/分 | 中位数/分 | 众数/分 | |
A校 | ______ | 85 | ______ |
B校 | 85 | ______ | 100 |
(2)结合两校成绩的平均数和中位数,分析哪个学校的决赛成绩较好;
(3)计算两校决赛成绩的方差,并判断哪个学校代表队选手成绩较为稳定.





