Question

某种规格小纸杯的侧面是由一半径为18cm、圆心角是60°的扇形OAB剪去一半径12cm的同心圆扇形OCD所围成的（不计接缝）（如图1）.

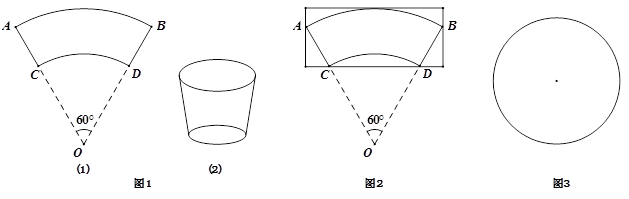
（1）求纸杯的底面半径和侧面积（结果保留π）

（2）要制作这样的纸杯侧面，如果按照图2所示的方式剪裁（不允许有拼接），至少要用多大的矩形纸片

（3）如图3，若在一张半径为18cm的圆形纸片上剪裁这样的纸杯侧面，最多能裁出多少个？

 

Answer 1

⑴2cm，30πcm^2，，⑵18cm和18-6cm，（3）9

解析:(1)设纸杯底面半径为r，

依题意，2πr=，r=2cm，----------2分

S_侧==π（18²-12²）=30πcm².------- ------4分

（2）连接AB，过O作OE⊥CD，交弧于F，

OA=OB，∠AOB=60度，

∴△ABO是等边三角形，∴AB=OA=18--------------5分

又∵△CDO也是等边三角形，

∴∠DCO=∠BAO，

∴AB∥CD，∴AB即为长方形的长.----- --------6分

OC=12，OE⊥CD，

∴CE=DE=6，

∴EO=6，∴EF=18-6.---------------8分

即所需长方形的两边长分别为：18cm和18-6cm.

（3）∵扇形OAB的圆心角为60度，∴在以O为圆心，18cm为半径的大圆和以12cm为半径的小圆组成的圆环中可剪出6个圆环（即小纸杯的侧面），如图.

剩下的一个半径12 cm 的圆中可按照如下方法剪圆环。作正六边形EFGHID，显然边长为12cm，将DE，FG，HI两边延长，相交于点A，B，C则以A、B、C为圆心18cm为半径画弧，三条弧相切于DE、FG、HI的中点，显然又可剪3个，

故最多可剪出9个纸杯的侧面.------- --------12分

 (1)根据纸杯的底面周长等于扇形OCD的弧长，可求得纸杯的底面半径，侧面积等于扇形OAB的面积-扇形OCD的面积，（2）、（3）根据垂径定理，等边三角形求解