Question

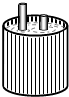如图，两根铁棒直立于桶底水平的木桶中，在桶中加入水后，一根露出水面的长度是它的

1

3

，另一根露出水面的长度是它的

1

5

．两根铁棒长度之和为55cm，此时木桶中水的深度是（　　）

A．20cm

B．25cm

C．30cm

D．35cm

Answer 1

分析：设较长铁棒的长度为xcm，较短铁棒的长度为ycm．因为两根铁棒之和为55cm，故可的方程：x+y=55，又知两棒未露出水面的长度相等，又可得方程

2

3

x=

4

5

y，把两个方程联立，组成方程组，解方程组可得较长的铁棒的长度，用较长的铁棒的长度×

2

3

可以求出木桶中水的深度．

解答：解：设较长铁棒的长度为xcm，较短铁棒的长度为ycm．
因为两根铁棒之和为55cm，故可列x+y=55，
又知两棒未露出水面的长度相等，故可知

2

3

x=

4

5

y，
据此可列：

x+y=55 2 3 x= 4 5 y

，
解得：

x=30 y=25

，
因此木桶中水的深度为30×

2

3

=20（cm）．
故选：A．．

点评：此题主要考查了二元一次方程组的应用，关键是弄清题意，找出合适的等量关系，列出方程组．