题目内容
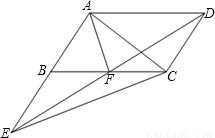
(2006•潍坊)已知平行四边形ABCD,AD=a,AB=b,∠ABC=α.点F为线段BC上一点(端点B,C除外),连接AF,AC,连接DF,并延长DF交AB的延长线于点E,连接CE.(1)当F为BC的中点时,求证:△EFC与△ABF的面积相等;
(2)当F为BC上任意一点时,△EFC与△ABF的面积还相等吗?说明理由.
【答案】分析:(1)S△EFC= FC•高h,S△ABF=
FC•高h,S△ABF= BF•高h′,而△EFC与△ABF的面积相等且当F为BC的中点,所以必须证明h=h′,而h=ABsinα,
BF•高h′,而△EFC与△ABF的面积相等且当F为BC的中点,所以必须证明h=h′,而h=ABsinα,
h′=EBsinα,所以证明方向转化为求证EB=AB,而EB=CD,可利用证△EBF≌△DCF来解答,因此便可求证所求;
(2)由于△ABC和△CDE为等底等高三角形,所以S△ABC=S△CDE,又因为△ACF和△CDF同底等高,所以S△AFC=S△CDF.
∴S△ABC-S△AFC=S△CDE-S△CDF,即S△ABF=S△EFC.
解答:(1)证明:∵点F为BC的中点,
∴BF=CF= BC=
BC=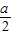 ,
,
又∵BF∥AD,
∴BE=AB=b,
∴A,E两点到BC的距离相等,都为bsinα,(3分)
则S△ABF= •
•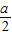 •bsinα=
•bsinα= absinα,
absinα,
S△EFC= •
•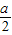 •bsinα=
•bsinα= absinα,
absinα,
∴S△ABF=S△EFC;(5分)
(2)解:
法一:当F为BC上任意一点时,
设BF=x,则FC=a-x,
∵四边形ABCD是平行四边形,
∴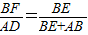 ,∴
,∴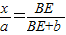 ,
,
∴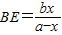 ,(7分)
,(7分)
在△EFC中,FC边上的高h1=BEsinα,
∴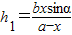 ,
,
∴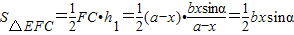 ,(9分)
,(9分)
又在△ABF中,BF边上的高h2=bsinα,
∴S△ABF= bxsinα,
bxsinα,
∴S△ABF=S△EFC;(11分)
法二:∵ABCD为平行四边形,
∴S△ABC=S△CDE= absinα,
absinα,
又∵S△AFC=S△CDF,
∴S△ABC-S△AFC=S△CDE-S△CDF,
即S△ABF=S△EFC.(11分)
点评:此题考查了平行四边形的基本性质和三角形全等的判定,难易程度适中.
 FC•高h,S△ABF=
FC•高h,S△ABF= BF•高h′,而△EFC与△ABF的面积相等且当F为BC的中点,所以必须证明h=h′,而h=ABsinα,
BF•高h′,而△EFC与△ABF的面积相等且当F为BC的中点,所以必须证明h=h′,而h=ABsinα,h′=EBsinα,所以证明方向转化为求证EB=AB,而EB=CD,可利用证△EBF≌△DCF来解答,因此便可求证所求;
(2)由于△ABC和△CDE为等底等高三角形,所以S△ABC=S△CDE,又因为△ACF和△CDF同底等高,所以S△AFC=S△CDF.
∴S△ABC-S△AFC=S△CDE-S△CDF,即S△ABF=S△EFC.
解答:(1)证明:∵点F为BC的中点,
∴BF=CF=
 BC=
BC=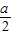 ,
,又∵BF∥AD,
∴BE=AB=b,
∴A,E两点到BC的距离相等,都为bsinα,(3分)
则S△ABF=
 •
•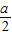 •bsinα=
•bsinα= absinα,
absinα,S△EFC=
 •
•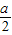 •bsinα=
•bsinα= absinα,
absinα,∴S△ABF=S△EFC;(5分)
(2)解:
法一:当F为BC上任意一点时,
设BF=x,则FC=a-x,
∵四边形ABCD是平行四边形,
∴
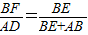 ,∴
,∴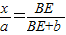 ,
,∴
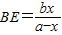 ,(7分)
,(7分)在△EFC中,FC边上的高h1=BEsinα,
∴
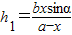 ,
,∴
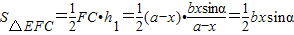 ,(9分)
,(9分)又在△ABF中,BF边上的高h2=bsinα,
∴S△ABF=
 bxsinα,
bxsinα,∴S△ABF=S△EFC;(11分)
法二:∵ABCD为平行四边形,
∴S△ABC=S△CDE=
 absinα,
absinα,又∵S△AFC=S△CDF,
∴S△ABC-S△AFC=S△CDE-S△CDF,
即S△ABF=S△EFC.(11分)
点评:此题考查了平行四边形的基本性质和三角形全等的判定,难易程度适中.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目


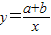 在同一坐标系中的图象不可能是( )
在同一坐标系中的图象不可能是( )

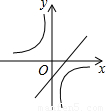

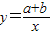 在同一坐标系中的图象不可能是( )
在同一坐标系中的图象不可能是( )