题目内容
若x、y、z满足3x+7y+z=1和4x+10y+z=2001，则分式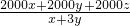
的值为________．
-3999
分析：分式=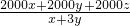
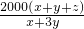，视x+3y与x+y+z为两个整体，对方程组进行整体改造后即可得出答案．
解答：由x、y、z满足3x+7y+z=1和4x+10y+z=2001，
得出：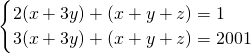
，解得：
，
∴=，
=
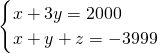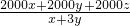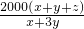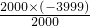=-3999．
故答案为：-3999．
点评：本题考查了分式的化简求值与三元一次方程组的应用，难度较大，关键是视x+3y与x+y+z为两个整体，对方程组进行整体改造．
分析：分式
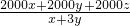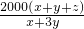=，视x+3y与x+y+z为两个整体，对方程组进行整体改造后即可得出答案．解答：由x、y、z满足3x+7y+z=1和4x+10y+z=2001，
得出：
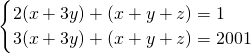，解得：，∴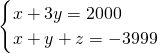
=，=
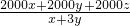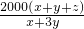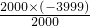=-3999．故答案为：-3999．
点评：本题考查了分式的化简求值与三元一次方程组的应用，难度较大，关键是视x+3y与x+y+z为两个整体，对方程组进行整体改造．
练习册系列答案
相关题目
已知x、y、z为三个非负实数，且满足3x+2y+z=5，2x+y-3z=1，若u=3x+y-7z，则u的最大值与最小值之和为（ ）
A、-
| ||
B、-
| ||
C、-
| ||
D、-
|