题目内容
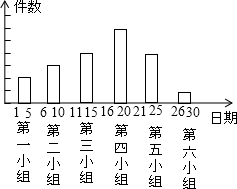
我校为了培养小能人、小发明家,开展了全校性的小制作比赛,作品上交时间为2010年3月1日至3月30日,组委会把同学们交来的作品按时间顺序每5天组成一组,对每一组的件数进行统计,绘制成如图所示的统计图.已知从左到右各矩形的高度比为2:3:4:6:4:1,其中第四小组交了18件作品.请你回答:
(1)本次活动共有
(2)经评比,第一组和第五组分别有3件和9件作品获奖,那么第一组和第五组的获奖率分别为
(3)小制作评比结束后,组委会评出了4件优秀的作品A、B、C、D,决定从中选出两件进行全校展示,请用树状图或列表法求出刚好展示作品A和作品C的概率.

(1)本次活动共有
60
60
件作品参赛:(2)经评比,第一组和第五组分别有3件和9件作品获奖,那么第一组和第五组的获奖率分别为
50%
50%
和75%
75%
;(3)小制作评比结束后,组委会评出了4件优秀的作品A、B、C、D,决定从中选出两件进行全校展示,请用树状图或列表法求出刚好展示作品A和作品C的概率.

分析:(1)用18除以第四小组所占的百分比,然后进行计算即可;
(2)求出这两个小组的作品数,然后根据百分比的求解方法列式进行计算即可得解;
(3)利用列表法列出所有可能情况,然后根据概率公式计算即可.
(2)求出这两个小组的作品数,然后根据百分比的求解方法列式进行计算即可得解;
(3)利用列表法列出所有可能情况,然后根据概率公式计算即可.
解答:解:(1)第四小组上交作品所占百分比为
×100%=30%,
18÷30%=60件;
(2)第一小组:上交作品
×2=6,
×100%=50%,
第五小组:上交作品
×4=12,
×100%=75%;
(3)列表如下:

共有12中情况,刚好展示A作品与C作品的情况有两种,
P(A、C)=
=
.
故答案为:(1)60,(2)50%,75%,(3)
.
| 6 |
| 2+3+4+6+4+1 |
18÷30%=60件;
(2)第一小组:上交作品
| 18 |
| 6 |
| 3 |
| 6 |
第五小组:上交作品
| 18 |
| 6 |
| 9 |
| 12 |
(3)列表如下:

共有12中情况,刚好展示A作品与C作品的情况有两种,
P(A、C)=
| 2 |
| 12 |
| 1 |
| 6 |
故答案为:(1)60,(2)50%,75%,(3)
| 1 |
| 6 |
点评:本题考查的是条形统计图的综合运用.读懂统计图,从统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数目.

练习册系列答案
相关题目