题目内容
【题目】如图1,分别以直角三角形三边为边向外作等边三角形,面积分别为S1、S2、S3;如图2,分别以直角三角形三个顶点为圆心,三边长为半径向外作圆心角相等的扇形,面积分别为S4、S5、S6 . 其中S1=16,S2=45,S5=11,S6=14,则S3+S4=( ) 
A.86
B.64
C.54
D.48
【答案】A
【解析】解:如图1,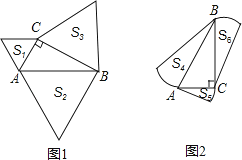
S1= ![]() AC2 , S2=
AC2 , S2= ![]() BC2 , S3=
BC2 , S3= ![]() AB2 .
AB2 .
∵AB2=AC2+BC2 ,
∴S1+S2=AC2+BC2=AB2=S3 ,
如图2,S4=S5+S6 ,
∴S3+S4=16+45+11+14=86.
故选A.
分别用AB、BC和AC表示出 S1、S2、S3 , 然后根据AB2=AC2+BC2即可得出S1、S2、S3的关系.同理,得出S4、S5、S6的关系.本题考查了勾股定理、等边三角形的性质.勾股定理:如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2 .

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目