题目内容
如图,一个长方形被划分成大小不等的6个正方形,已知中间的最小的正方形的面积为1平方厘米,则这个长方形的面积为 平方厘米.
【答案】分析:本题可设这6个正方形中最大的一个边长为x,根据矩形的性质列方程从而求得长方形的面积.
解答:解:设这6个正方形中最大的一个边长为x,
∵图中最小正方形边长是1,
∴其余的正方形边长分别为x-1,x-2,x-3,x-3,
∴x+x-1=2(x-3)+x-2,
∴x=7,
∴长方形的长为x+x-1=13,宽为x+x-3=11,面积为13×11=143平方厘米.
故答案为:143.
点评:此类题目属于数形结合,需仔细分析图形,从中找出有关信息,并利用方程解决问题.
解答:解:设这6个正方形中最大的一个边长为x,
∵图中最小正方形边长是1,
∴其余的正方形边长分别为x-1,x-2,x-3,x-3,
∴x+x-1=2(x-3)+x-2,
∴x=7,
∴长方形的长为x+x-1=13,宽为x+x-3=11,面积为13×11=143平方厘米.
故答案为:143.
点评:此类题目属于数形结合,需仔细分析图形,从中找出有关信息,并利用方程解决问题.

练习册系列答案
相关题目
 如图,一个长方形被分成4个面积不相等的小长方形,其中A、B、的面积分别是A=160,B=172,C=215,(单位:平方厘米).原来大长方形的面积是
如图,一个长方形被分成4个面积不相等的小长方形,其中A、B、的面积分别是A=160,B=172,C=215,(单位:平方厘米).原来大长方形的面积是 6、如图,一个长方形被分成四块,其中三块面积分别是25,20,30,则第四块面积是
6、如图,一个长方形被分成四块,其中三块面积分别是25,20,30,则第四块面积是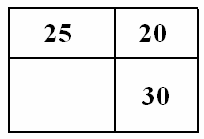
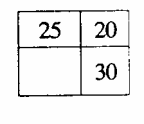
 如图,一个长方形被分成4个面积不相等的小长方形,其中A、B、的面积分别是A=160,B=172,C=215,(单位:平方厘米).原来大长方形的面积是________平方厘米.
如图,一个长方形被分成4个面积不相等的小长方形,其中A、B、的面积分别是A=160,B=172,C=215,(单位:平方厘米).原来大长方形的面积是________平方厘米.