题目内容
 (2013•江西)如图,矩形ABCD中,点E、F分别是AB、CD的中点,连接DE和BF,分别取DE、BF的中点M、N,连接AM,CN,MN,若AB=2
(2013•江西)如图,矩形ABCD中,点E、F分别是AB、CD的中点,连接DE和BF,分别取DE、BF的中点M、N,连接AM,CN,MN,若AB=2| 2 |
| 3 |
2
| 6 |
2
.| 6 |
分析:根据矩形的中心对称性判定阴影部分的面积等于空白部分的面积,从而得到阴影部分的面积等于矩形的面积的一半,再根据矩形的面积公式列式计算即可得解.
解答:解:∵点E、F分别是AB、CD的中点,M、N分别为DE、BF的中点,
∴矩形绕中心旋转180°阴影部分恰好能够与空白部分重合,
∴阴影部分的面积等于空白部分的面积,
∴阴影部分的面积=
×矩形的面积,
∵AB=2
,BC=2
,
∴阴影部分的面积=
×2
×2
=2
.
故答案为:2
.
∴矩形绕中心旋转180°阴影部分恰好能够与空白部分重合,
∴阴影部分的面积等于空白部分的面积,
∴阴影部分的面积=
| 1 |
| 2 |
∵AB=2
| 2 |
| 3 |
∴阴影部分的面积=
| 1 |
| 2 |
| 2 |
| 3 |
| 6 |
故答案为:2
| 6 |
点评:本题考查了矩形的性质,主要利用了矩形的中心对称性,判断出阴影部分的面积等于矩形的面积的一半是解题的关键.

练习册系列答案
相关题目
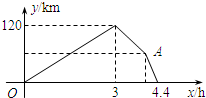 车之间的距离y(km)与乙车行驶时间x(h)之间的函数图象.以下结论正确的是
车之间的距离y(km)与乙车行驶时间x(h)之间的函数图象.以下结论正确的是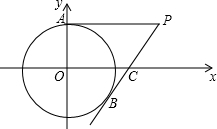 (2013•江西)如图,在平面直角坐标系中,以点O为圆心,半径为2的圆与y轴交点A,点P(4,2)是⊙O外一点,连接AP,直线PB与⊙O相切于点B,交x轴于点C.
(2013•江西)如图,在平面直角坐标系中,以点O为圆心,半径为2的圆与y轴交点A,点P(4,2)是⊙O外一点,连接AP,直线PB与⊙O相切于点B,交x轴于点C.
 (2013•江西)如图,?ABCD与?DCFE的周长相等,且∠BAD=60°,∠F=110°,则∠DAE的度数为
(2013•江西)如图,?ABCD与?DCFE的周长相等,且∠BAD=60°,∠F=110°,则∠DAE的度数为