题目内容
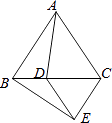
【题目】已知,如图1:△ABC中,∠B、∠C的平分线相交于点O,过点O作EF∥BC交AB、AC于E、F.
(1)直接写出图1中所有的等腰三角形,并指出EF与BE、CF间有怎样的数量关系?
(2)在(1)的条件下,若AB=10,AC=15,求△AEF的周长.
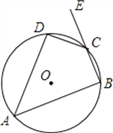
(3)如图2,若△ABC中,∠B的平分线与三角形外角∠ACG的平分线CO交于点O,过O点作OE∥BC交AB于E,交AC于F,请问(1)中EF与BE、CF间的关系还是否存在,若存在,说明理由;若不存在,写出三者新的数量关系,并说明理由.
【答案】
(1)解:有2个等腰三角形分别是:等腰△OBE和等腰△OCF,
EF=BE+CF.
(2)解:△AEF的周长为AE+AF+EF=AE+AF+OE+OF=AE+AF+BE+CF=AB+AC=25
(3)解:(1)中EF与BE,CF间的关系不存在,新的数量关系为:EF=BE-CF,
证明:由BO平分∠ABC及OE∥BC可证BE=EO,
由CO平分∠ACG及OE∥BC可证CF=FO,
而EO=EF+OF,则EF=EO-OF=BE-CF
【解析】(1) 根据已知条件∠B、∠C的平分线相交于点O,及EF∥BC,可证得∠EBO=∠EOB,∠FCO=∠FOC,得出OE=BE,OF=FC,即可证得△OBE和△OCF是等腰三角形,及EF=BE+CF。
(2)由(1)可知EF=BE+CF,得出△AEF的周长=AB+AC,代入计算即可得出结果。
(3)根据已知条件可知新的数量关系为:EF=BE-CF,先证明BE=EO,CF=FO,再由EO=EF+OF,就可得出EF==BE-CF。

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目