题目内容
【题目】如图,在矩形ABCD中,AD=5,AB=8,点E是DC上一点,将∠D沿折痕AE折叠,使点D落在点D′处,当△AD′B为等腰三角形时,则DE的长为______________.
【答案】![]() 或16﹣
或16﹣![]() .
.
【解析】
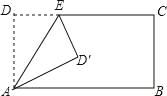
试题分析:①当AD′=D′B=5时,过点D′作MN⊥AB于点N,MN交CD于点M,如图1所示.设DE=a,则D′E=a.∵将∠D沿折痕AE折叠,使点D落在点D′处,∴AN=DM=![]() CD=
CD=![]() AB=4,AD=AD′=5,由勾股定理可知:ND′=
AB=4,AD=AD′=5,由勾股定理可知:ND′=![]() =3,∴MD′=MN﹣ND′=AD﹣ND′=2,EM=DM﹣DE=4﹣a,∵ED′2=EM2+MD′2,即a2=(4﹣a)2+4,解得:a=
=3,∴MD′=MN﹣ND′=AD﹣ND′=2,EM=DM﹣DE=4﹣a,∵ED′2=EM2+MD′2,即a2=(4﹣a)2+4,解得:a=![]() ;
;
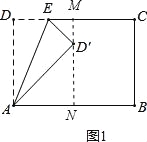
②当AB=D′B=8时,过点D′作MN⊥AB于点N,MN交CD于点M,如图2所示.设DE=a,则D′E=a.∵将∠D沿折痕AE折叠,使点D落在点D′处,∴AD′=AD=5,∴AD′2﹣AN2=BD′2﹣BN2,即52﹣AN2=82﹣(8﹣AN)2,∴AN=![]() ,∴BN=
,∴BN=![]() ,∴D′N=
,∴D′N=![]() ,∵∠MED′+∠ED′M=∠ED′M+∠AD′N=90°,∴∠MED′=∠AD′N,∴△EMD′∽△AD′N,∴
,∵∠MED′+∠ED′M=∠ED′M+∠AD′N=90°,∴∠MED′=∠AD′N,∴△EMD′∽△AD′N,∴![]() ,即
,即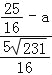 =
=![]() ,∴a=16﹣
,∴a=16﹣![]() ,∴当△AD′B为等腰三角形时,则DE的长为
,∴当△AD′B为等腰三角形时,则DE的长为![]() 或16﹣
或16﹣![]() .故答案为:
.故答案为:![]() 或16﹣
或16﹣![]() .
.


练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目