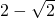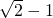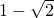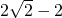题目内容
 如图,⊙O上B、D两点位于弦AC的两侧,
如图,⊙O上B、D两点位于弦AC的两侧, ,若∠D=62°,则∠AOB=________.
,若∠D=62°,则∠AOB=________.
62°
分析:连接OC.根据同弧所对的圆周角是所对的圆心角的一半知∠D= ∠AOC,等弧所对的圆心角相等推知∠AOB=∠BOC,从而知∠AOB=∠D=62°.
∠AOC,等弧所对的圆心角相等推知∠AOB=∠BOC,从而知∠AOB=∠D=62°.
解答: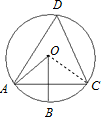 解:连接OC.
解:连接OC.
∵∠D= ∠AOC(同弧所对的圆周角是所对的圆心角的一半);
∠AOC(同弧所对的圆周角是所对的圆心角的一半);
又∵ (已知),
(已知),
∴∠AOB=∠BOC(等弧所对的圆心角相等);
∴∠AOB=∠D=62°.
故答案是:62°.
点评:本题考查了圆心角、弧、弦的关系.在同圆或等圆中,如果①两个圆心角,②两条弧,③两条弦中,有一组量相等,那么它们所对应的其余各组量都分别相等;
圆心角、弧、弦的不等量关系:在同圆或等圆中,如果圆心角不相等,那么圆心角所对的弧、弦、弦的弦心距也不相等,圆心角所对的弧大,所对的弦大,所对的弦的弦心距反而小.
需注意的是“在同圆或等圆中”的前提条件不能丢.
分析:连接OC.根据同弧所对的圆周角是所对的圆心角的一半知∠D=
 ∠AOC,等弧所对的圆心角相等推知∠AOB=∠BOC,从而知∠AOB=∠D=62°.
∠AOC,等弧所对的圆心角相等推知∠AOB=∠BOC,从而知∠AOB=∠D=62°.解答:
 解:连接OC.
解:连接OC.∵∠D=
 ∠AOC(同弧所对的圆周角是所对的圆心角的一半);
∠AOC(同弧所对的圆周角是所对的圆心角的一半);又∵
 (已知),
(已知),∴∠AOB=∠BOC(等弧所对的圆心角相等);
∴∠AOB=∠D=62°.
故答案是:62°.
点评:本题考查了圆心角、弧、弦的关系.在同圆或等圆中,如果①两个圆心角,②两条弧,③两条弦中,有一组量相等,那么它们所对应的其余各组量都分别相等;
圆心角、弧、弦的不等量关系:在同圆或等圆中,如果圆心角不相等,那么圆心角所对的弧、弦、弦的弦心距也不相等,圆心角所对的弧大,所对的弦大,所对的弦的弦心距反而小.
需注意的是“在同圆或等圆中”的前提条件不能丢.

练习册系列答案
相关题目

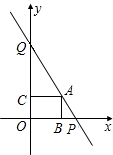 如图,直线y=-2x+8与两坐标轴分别交于P,Q两点,在线段PQ上有一点A,过点A分别作两坐标轴的垂线,垂足分别为B、C.
如图,直线y=-2x+8与两坐标轴分别交于P,Q两点,在线段PQ上有一点A,过点A分别作两坐标轴的垂线,垂足分别为B、C.

 两个实数对应的点分别为A、B,点C与点B关于点A对称(即AB=AC),则点C表示的数是
两个实数对应的点分别为A、B,点C与点B关于点A对称(即AB=AC),则点C表示的数是