题目内容
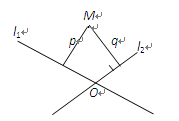
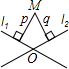
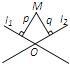 10、如图,在平面内,两条直线l1,l2相交于点O,对于平面内任意一点M,若p,q分别是点M到直线l1,l2的距离,则称(p,q)为点M的“距离坐标”.根据上述规定,“距离坐标”是(2,1)的点共有( )个.
10、如图,在平面内,两条直线l1,l2相交于点O,对于平面内任意一点M,若p,q分别是点M到直线l1,l2的距离,则称(p,q)为点M的“距离坐标”.根据上述规定,“距离坐标”是(2,1)的点共有( )个.分析:到l1距离为2的直线有2条,到l2距离为3的直线有2条,这4条直线有4个交点,这4个交点就是“距离坐标”是(2,1)的点.
解答:解:因为两条直线相交有四个角,因此每一个角内就有一个距离坐标是(2,1)的点,共4个.
故选D.
故选D.
点评:本题用到的知识点为:到一条已知直线距离为定值的直线有两条.

练习册系列答案
相关题目
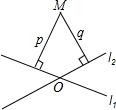 如图,在平面内,两条直线l1,l2相交于点O,对于平面内任意一点M,若p、q分别是点M到直线l1,l2的距离,则称(p,q)为点M的“距离坐标”.根据上述规定,“距离坐标”是(1,1)的点共有
如图,在平面内,两条直线l1,l2相交于点O,对于平面内任意一点M,若p、q分别是点M到直线l1,l2的距离,则称(p,q)为点M的“距离坐标”.根据上述规定,“距离坐标”是(1,1)的点共有4
4
个. 18、如图,在平面内,两条直线l1,l2相交于点O,对于平面内任意一点M,若p,q分别是点M到直线l1,l2的距离,则称(p,q)为点M的“距离坐标”.根据上述规定,“距离坐标”是(2,1)的点共有
18、如图,在平面内,两条直线l1,l2相交于点O,对于平面内任意一点M,若p,q分别是点M到直线l1,l2的距离,则称(p,q)为点M的“距离坐标”.根据上述规定,“距离坐标”是(2,1)的点共有