��Ŀ����
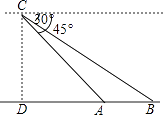
����Ŀ����֪����ͼ��OΪ����ԭ�����ı���OABCΪ������A��10��0����C��0��4������D��OA�е�����P��BC����ÿ��1����λ���ٶ���C��B�˶������˶�ʱ��Ϊt�룮

��1����ODP�����S=________��
��2��tΪ��ֵʱ���ı���PODB��ƽ���ı��Σ�
��3�����߶�PB���Ƿ����һ��Q��ʹ��ODQPΪ���Σ�����������t��ֵ�������Q���������������������˵��������
��4������OPDΪ��������������д���������������ĵ�P�����꣨��ֱ��д����������д���̣�
���𰸡���1��10����2��5����3����8��4������4�����������ĵ�P������ΪP1��3��4����P2��2.5��4����P3��2��4����P4��8��4��.
��������
������1�����������ε������ʽ���������ODP�����S��
��2������PB��OD������ƽ���ı��ε��ж���֪��PB=OD=5ʱ���ı���PODB��ƽ���ı��Σ������PC=5���Ӷ����t��ֵ��
��3���������ε��ж�����OD=OP=PQ=5ʱ���ı���ODQPΪ���Σ���Rt��OPC�У����ù��ɶ������CP��ֵ���������t��ֵ��Q������ꣻ
��4������OPDΪ����������ʱ������������������ۣ������OΪ���㣬��ôOP=OD=5�������PΪ���㣬��ôPO=PD�������DΪ���㣬��ôDP=DO=5���ֱ��������ߣ����ù��ɶ������P�������.
�����������1����OΪ����ԭ�㣬A��10��0�����ı���OABCΪ���Σ�C��0��4����
��OA=BC=10��OC=4��
����D��OA�е㣬
��OD=DA= ![]() OA=5��
OA=5��
���ODP�����S= ![]() ODOC=
ODOC= ![]() ��5��4=10��
��5��4=10��
��2���⣺��PB��OD��
�൱PB=ODʱ���ı���PODB��ƽ���ı��Σ�
��OD=5��
��PB=5��
��PC=BC��PB=10��5=5��
�ߵ�P��BC����ÿ��1����λ���ٶ���C��B�˶���
��t=5
��3���⣺��OD=OP=PQ=5ʱ��ODQPΪ���Σ�
��Rt��OPC�У��ɹ��ɶ����ã�
PC= ![]() =
= ![]() =3��
=3��
��t=3��CQ=CP+PQ=3+5=8��
��Q���������8��4��
��4���⣺��OPDΪ����������ʱ�������������
�����OΪ���㣬��ôOP=OD=5��
�ɹ��ɶ����������PC=3����ʱP1��3��4����
�����PΪ���㣬��ôPO=PD��
��PE��OA��E����OE=ED=2.5����ʱP2��2.5��4����
�����DΪ���㣬��ôDP=DO=5��
��DF��BC��F���ɹ��ɶ�������PF=3��
��P3C=5��3=2��P4C=5+3=8����ʱP3��2��4����P4��8��4����
�������������������ĵ�P������ΪP1��3��4����P2��2.5��4����P3��2��4����P4��8��4����