题目内容
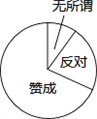
 为了鼓励学生课外阅读,学校公布了“阅读”奖励计划方案,征求学生的意见,赞成:反对、无所谓三种意见的人数之比为7:2:1.如图所示的扇形图表示上述分布情况:
为了鼓励学生课外阅读,学校公布了“阅读”奖励计划方案,征求学生的意见,赞成:反对、无所谓三种意见的人数之比为7:2:1.如图所示的扇形图表示上述分布情况:(1)如果持反对意见的有180人,求这个学校的学生总数;
(2)求各个扇形的圆心角的度数.
分析:分析扇形图可知:反对的占
,人数为180人,则总人数为180÷
=900人;
第(2)问,可先求出每一份所占圆心角的度数,然后再计算所求结果.
| 2 |
| 10 |
| 2 |
| 10 |
第(2)问,可先求出每一份所占圆心角的度数,然后再计算所求结果.
解答:解:(1)由题意知:180÷2=90
∴90×10=900
所以这个学校的学生总数是900人;
(2)
= 36°
则持赞成意见的占的圆心角度数为36°×7=252°,
持反对意见的占的圆心角度数为36°×2=72°,
持无所谓意见的占的圆心角度数为36°×1=36°.
∴90×10=900
所以这个学校的学生总数是900人;
(2)
| 360° |
| 10 |
则持赞成意见的占的圆心角度数为36°×7=252°,
持反对意见的占的圆心角度数为36°×2=72°,
持无所谓意见的占的圆心角度数为36°×1=36°.
点评:本题考查扇形统计图及相关计算.在扇形统计图中,每部分占总部分的百分比等于该部分所对应的扇形圆心角的度数与360°的比.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
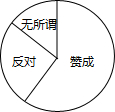 三种意见的人数之比为7:2:1,如图所示的扇形统计图表示上述分布情况:
三种意见的人数之比为7:2:1,如图所示的扇形统计图表示上述分布情况: