题目内容
 如图,AB是半圆的直径,点C是弧AB的中点,点E是弧AC的中点,连接EB,CA交于点F,则
如图,AB是半圆的直径,点C是弧AB的中点,点E是弧AC的中点,连接EB,CA交于点F,则| EF |
| BF |
A、
| ||||
B、
| ||||
C、1-
| ||||
D、
|
分析:根据平行线的性质证得,△ADE是等腰直角三角形,求得BE=
+1,再证△AEF∽△BEA,得EF=
=
-1,BF=2.所以
=
.
| 2 |
| 1 | ||
|
| 2 |
| EF |
| BF |
| ||
| 2 |
解答: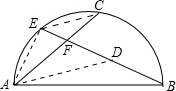 解:方法1:连接AE、CE,作AD∥CE,交BE于D.
解:方法1:连接AE、CE,作AD∥CE,交BE于D.
∵点E是弧AC的中点
∴可设AE=CE=1,
根据平行线的性质得∠ADE=∠CED=45°.
∴△ADE是等腰直角三角形,
则AD=
,BD=AD=
.
所以BE=
+1.
再根据两角对应相等得△AEF∽△BEA,
则EF=
=
-1,BF=2.
所以
=
.
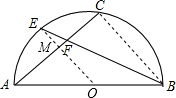 方法2:连接OE,BC,OE与AC交于点M.
方法2:连接OE,BC,OE与AC交于点M.
∵E为弧AC的中点,
易证OE⊥AC,
∵∠C=90°,∠AOE=45°,
∴OE∥BC,
设OM=1,则AM=1,
∴AC=BC=2,OA=
,
∴OE=
,
∴EM=
-1,
∵OE∥BC,
∴
=
=
.
故选D.
 解:方法1:连接AE、CE,作AD∥CE,交BE于D.
解:方法1:连接AE、CE,作AD∥CE,交BE于D.∵点E是弧AC的中点
∴可设AE=CE=1,
根据平行线的性质得∠ADE=∠CED=45°.
∴△ADE是等腰直角三角形,
则AD=
| 2 |
| 2 |
所以BE=
| 2 |
再根据两角对应相等得△AEF∽△BEA,
则EF=
| 1 | ||
|
| 2 |
所以
| EF |
| BF |
| ||
| 2 |
 方法2:连接OE,BC,OE与AC交于点M.
方法2:连接OE,BC,OE与AC交于点M.∵E为弧AC的中点,
易证OE⊥AC,
∵∠C=90°,∠AOE=45°,
∴OE∥BC,
设OM=1,则AM=1,
∴AC=BC=2,OA=
| 2 |
∴OE=
| 2 |
∴EM=
| 2 |
∵OE∥BC,
∴
| EF |
| BF |
| EM |
| BC |
| ||
| 2 |
故选D.
点评:此题要能够根据弧之间的关系找到角之间的关系,熟练运用圆周角定理的推论,能够根据相似三角形的性质建立对应边之间的关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 道BC的长86.96米,跑道的宽为l米.(π=3.14,结果精确到0.01)
道BC的长86.96米,跑道的宽为l米.(π=3.14,结果精确到0.01)


