题目内容
【题目】已知正方形ABCD和正方形AEFG有公共顶点A,将正方形AEFG绕点A旋转.
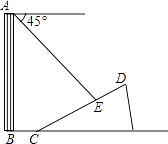
(1)发现:如图1,当E点旋转到DA的延长线上时,△ABE与△ADG的面积关系是:;
(2)引申:当正方形AEFG旋转任意一个角度时,△ABE与△ADG的面积关系是:;
(3)如图3,四边形ABMN、四边形DEAC、四边形BFGC均为正方形,则S△ABC、S△AEN、S△BMF、S△DCG的关系是;
(4)运用:某小区中有一块空地,要在其中建三个正方形健身场所(如图3),其余空地修成草坪.若已知其中一个正方形的边长为5m,另一个正方形的边长为4m,则草坪的最大面积是 .
【答案】
(1)△ABE的面积=△ADG的面积
(2)△ABE的面积=△ADG的面积
(3)S△ABC=S△AEN=S△BMF=S△DCG
(4)30m2
【解析】解:(1)∵正方形ABCD和正方形AEFG有公顶点A,将正方形AEFG绕点A旋转,E点旋转到DA的延长线上
∴AE=AG,AB=AD,∠EAB=∠GAD=90°,
在△ABE和△ADG中 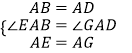
∴△ABE≌△ADG(SAS),
∴△ABE的面积=△ADG的面积;
所以答案是:△ABE的面积=△ADG的面积;
⑵结论仍然成立.理由如下:
作GH⊥DA交DA的延长线于H,EP⊥BA交BA的延长线于P,如图所示,
∵∠PAD=90°,∠EAG=90°,
∴∠PAE=∠GAH,
在△AHG和△AEP中, 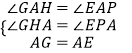 ,
,
∴△AHG≌△AEP(AAS),
∴GH=BP,
∵△ABE的面积= ![]() EPAB,△ADG的面积=
EPAB,△ADG的面积= ![]() GHAD,
GHAD,
∴△ABE的面积=△ADG的面积;
所以答案是:△ABE的面积=△ADG的面积;
⑶由(2)得:S△ABC=S△AEN=S△BMF=S△DCG ,
所以答案是:S△ABC=S△AEN=S△BMF=S△DCG ,
⑷∵AB=5m,AC=4m,
∴△ABC的面积= ![]() ×5×4×sin∠BAC=10sin∠BAC,
×5×4×sin∠BAC=10sin∠BAC,
当sin∠BAC=1时,△ABC的面积的最大值为10,
根据(2)中的结论得到阴影部分的面积和的最大值=△ABC的面积的3倍=3×10=30m2 .
所以答案是:30m2 . 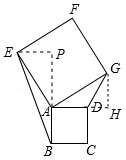
【考点精析】认真审题,首先需要了解正方形的性质(正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形),还要掌握锐角三角函数的定义(锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数)的相关知识才是答题的关键.

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案