题目内容
 如图,D,E分别△ABC的边AB,AC的中点,给出下列结论:①BC=2DE;②△ADE∽△ABC;③AD:AE=AB:AC;④S△ADE:S四边形BCED=1:3.其中正确的结论有
如图,D,E分别△ABC的边AB,AC的中点,给出下列结论:①BC=2DE;②△ADE∽△ABC;③AD:AE=AB:AC;④S△ADE:S四边形BCED=1:3.其中正确的结论有
- A.4个
- B.3个
- C.2个
- D.1个
A
分析:根据D,E分别是△ABC的边AB,AC的中点,得到DE是△ABC的中位线,再利用中位线的性质得到DE与BC的关系,判断三角形相似,根据相似三角形的性质对所给命题进行判断.
解答:∵D,E分别是△ABC的边AB,AC的中点,
∴DE是△ABC的中位线,
∴DE= BC,DE∥BC.
BC,DE∥BC.
∵DE= BC,
BC,
∴BC=2DE.
∴①正确.
∵DE∥BC,
∴△ADE∽△ABC.
∴②正确.
∵△ADE∽△ABC,
∴AD:AE=AB:AC,
∴③正确.
∵DE:BC=1:2,又△ADE∽△ABC,
∴S△ADE:S△ABC=1:4,
∴S△ADE:S四边形BCED=1:3.
∴④正确.
故选A.
点评:本题考查的是相似三角形的判定与性质,根据题意得到DE是三角形的中位线,再用中位线的性质判定相似三角形,然后用相似三角形的性质判定三角形与四边形的面积关系.
分析:根据D,E分别是△ABC的边AB,AC的中点,得到DE是△ABC的中位线,再利用中位线的性质得到DE与BC的关系,判断三角形相似,根据相似三角形的性质对所给命题进行判断.
解答:∵D,E分别是△ABC的边AB,AC的中点,
∴DE是△ABC的中位线,
∴DE=
 BC,DE∥BC.
BC,DE∥BC.∵DE=
 BC,
BC,∴BC=2DE.
∴①正确.
∵DE∥BC,
∴△ADE∽△ABC.
∴②正确.
∵△ADE∽△ABC,
∴AD:AE=AB:AC,
∴③正确.
∵DE:BC=1:2,又△ADE∽△ABC,
∴S△ADE:S△ABC=1:4,
∴S△ADE:S四边形BCED=1:3.
∴④正确.
故选A.
点评:本题考查的是相似三角形的判定与性质,根据题意得到DE是三角形的中位线,再用中位线的性质判定相似三角形,然后用相似三角形的性质判定三角形与四边形的面积关系.

练习册系列答案
相关题目
 如图,E、F分别在AD、BC上,EFCD是正方形,且矩形ABCD∽矩形AEFB,则BC:AB的值是
如图,E、F分别在AD、BC上,EFCD是正方形,且矩形ABCD∽矩形AEFB,则BC:AB的值是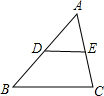 如图,D、E分别在△ABC的边AB、AC上,且AD=
如图,D、E分别在△ABC的边AB、AC上,且AD= (2013•白云区一模)已知,如图,E、F分别为矩形ABCD的边AD和BC上的点,AE=CF.求证:BE=DF.
(2013•白云区一模)已知,如图,E、F分别为矩形ABCD的边AD和BC上的点,AE=CF.求证:BE=DF. 如图,D、E分别为△ABC的边AB、BC的中点,若AC=12cm,∠A=45°,则DE=
如图,D、E分别为△ABC的边AB、BC的中点,若AC=12cm,∠A=45°,则DE=