题目内容
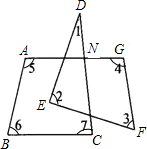
如图,若∠1+∠2+∠3+∠4+∠5+∠6+∠7=n•90°,则n为( )
| A.4 | B.5 | C.6 | D.7 |

设AG与DE交于点M,与DC交于点N,
则∠5+∠6+∠7=360°-∠ANC,∠2+∠3+∠4=360°-∠EMG,
则∠1+∠2+∠3+∠4+∠5+∠6+∠7=∠1+(360°-∠ANC)+(360°-∠EMG)=720°+∠1-∠ANC-∠EMG=720°+∠1-(180°-∠DMN)-(180°-∠DNM)=360°+(∠1+∠DMN+∠DNM)=360°+180°=540°.
又因∠1+∠2+∠3+∠4+∠5+∠6+∠7=540°=n•90°,
所以n=6.
故选C.
则∠5+∠6+∠7=360°-∠ANC,∠2+∠3+∠4=360°-∠EMG,
则∠1+∠2+∠3+∠4+∠5+∠6+∠7=∠1+(360°-∠ANC)+(360°-∠EMG)=720°+∠1-∠ANC-∠EMG=720°+∠1-(180°-∠DMN)-(180°-∠DNM)=360°+(∠1+∠DMN+∠DNM)=360°+180°=540°.
又因∠1+∠2+∠3+∠4+∠5+∠6+∠7=540°=n•90°,
所以n=6.
故选C.

练习册系列答案
相关题目
