题目内容
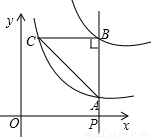
(2009•衢江区一模)如图,P为x轴正半轴上一点,过点P作x轴的垂线,交函数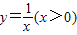 的图象于点A,交函数
的图象于点A,交函数 的图象于点B,过点B作x轴的平行线,交
的图象于点B,过点B作x轴的平行线,交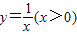 于点C,连接AC.
于点C,连接AC.(1)当点P的坐标为(2,0)时,求△ABC的面积;
(2)当点P的坐标为(t,0)时,△ABC的面积是否随t值的变化而变化?
【答案】分析:(1)根据点P的坐标和函数的解析式可以分别求得点A、B、C的坐标,进一步求得三角形的面积;
(2)根据(1)中的方法进行求解,看最后的结果是否为一个定值即可.
解答:解:(1)根据题意,得点A、B的横坐标和点P的横坐标相等,即为2.
∵点A在函数 的双曲线上,
的双曲线上,
∴A点纵坐标是 ,
,
∵点B在函数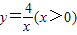 的图象上
的图象上
∴B点的纵坐标是2.
∴点C的纵坐标是2,
∵点C在函数 的双曲线上
的双曲线上
∴C点横坐标是 .
.
∴AB= ,BC=
,BC=
∴△ABC的面积是: =
= .
.
(2)根据(1)中的思路,可以分别求得点A(t, ),B(t,
),B(t, ),C(
),C( ,
, ).
).
∴AB= ,BC=
,BC= t,
t,
∴△ABC的面积是 .
.
∴△ABC的面积不会随着t的变化而变化.
点评:解答此题时要能够根据解析式熟练地求得各个点的坐标,根据坐标计算线段的长度.
(2)根据(1)中的方法进行求解,看最后的结果是否为一个定值即可.
解答:解:(1)根据题意,得点A、B的横坐标和点P的横坐标相等,即为2.
∵点A在函数
 的双曲线上,
的双曲线上,∴A点纵坐标是
 ,
,∵点B在函数
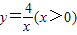 的图象上
的图象上∴B点的纵坐标是2.
∴点C的纵坐标是2,
∵点C在函数
 的双曲线上
的双曲线上∴C点横坐标是
 .
.∴AB=
 ,BC=
,BC=
∴△ABC的面积是:
 =
= .
.(2)根据(1)中的思路,可以分别求得点A(t,
 ),B(t,
),B(t, ),C(
),C( ,
, ).
).∴AB=
 ,BC=
,BC= t,
t,∴△ABC的面积是
 .
.∴△ABC的面积不会随着t的变化而变化.
点评:解答此题时要能够根据解析式熟练地求得各个点的坐标,根据坐标计算线段的长度.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
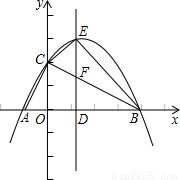
 x2+
x2+ x+2交x轴于A、B两点,交y轴于点C.
x+2交x轴于A、B两点,交y轴于点C.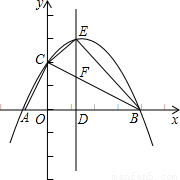
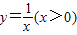 的图象于点A,交函数
的图象于点A,交函数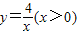 的图象于点B,过点B作x轴的平行线,交
的图象于点B,过点B作x轴的平行线,交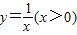 于点C,连接AC.
于点C,连接AC.
 x2+
x2+ x+2交x轴于A、B两点,交y轴于点C.
x+2交x轴于A、B两点,交y轴于点C.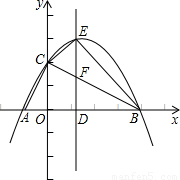
 x2+
x2+ x+2交x轴于A、B两点,交y轴于点C.
x+2交x轴于A、B两点,交y轴于点C.