题目内容
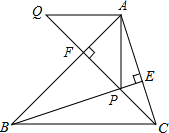
【题目】如图,BE、CF是△ABC的高且相交于点P,AQ∥BC交CF延长线于点Q,若有BP=AC,CQ=AB,线段AP与AQ的关系如何?说明理由。
【答案】证明见解析
【解析】试题分析:
由BE、CF是△ABC的高,易得∠ABP+∠BPF=90°,∠ACP+∠CPE=90°,结合∠BPF=∠CPE,易得∠ABP=∠ACP,这样结合BP=AC,CQ=AB,即可由“SAS”证得△ACQ≌△PBA,从而可得AP=AQ,∠Q=∠PAF,结合∠PAF+∠APF=90°,可得:∠APF+∠Q=90°,即可得到∠QAP=90°,从而可得AQ⊥AP,由此即可得到AQ与AP的关系是相等且互相垂直.
试题解析:
AQ与AP的关系是:相等且互相垂直,理由如下:
∵BE、CF是△ABC的高,
∴∠BFP=∠CEP=90°,
∴∠ABP+∠BPF=90°,∠ACP+∠CPE=90°,
又∵∠BPF=∠CPE,
∴∠ABP=∠ACP,
在△ACQ和△PBA中:
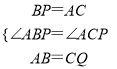 ,
,
∴△ACQ≌△PBA(SAS),
∴AP=AQ,∠Q=∠PAF,
∵∠PAF+∠APF=90°,
∴∠APF+∠Q=90°,
∴AP⊥AQ,即:AQ与AP的关系是相等且互相垂直.

练习册系列答案
相关题目
【题目】根据科学研究表明,在弹簧的承受范围内,弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂的物体的重量x(kg)间有下表的关系:下列说法不正确的是( )
x/kg | 0 | 1 | 2 | 3 | 4 | 5 |
y/cm | 20 | 20.5 | 21 | 21.5 | 22 | 22.5 |
A. 弹簧不挂重物时的长度为0cm
B. x与y都是变量,且x是自变量,y是因变量
C. 随着所挂物体的重量增加,弹簧长度逐渐边长
D. 所挂物体的重量每增加1kg,弹簧长度增加0.5cm