题目内容
如图，正方体的每个面上都写有一个实数，已知相对的两个面上的两数之和相等，若15、9、-4的对面的数分别是x、y、z，则2x-3y+z的值为 ．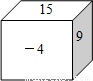
【答案】分析：根据向对面上的数字的和相等列出等式并设它们的和等于k，然后用k表示出x、y、z，再代入代数式计算，正好消掉k，即可得解．
解答：解：设相对面上的两个数的和等于k，
∵相对的两个面上的两数之和相等，
∴x+15=y+9=z-4=k，
∴x=k-15，y=k-9，z=k+4，
∴2x-3y+z=2（k-15）-3（k-9）+k+4=2k-30-3k+27+k+4=1．
故答案为：1．
点评：本题考查了正方体相对面上的文字，设相对面上的两个数的和等于k，然后用k表示出x、y、z是解题的关键．
解答：解：设相对面上的两个数的和等于k，
∵相对的两个面上的两数之和相等，
∴x+15=y+9=z-4=k，
∴x=k-15，y=k-9，z=k+4，
∴2x-3y+z=2（k-15）-3（k-9）+k+4=2k-30-3k+27+k+4=1．
故答案为：1．
点评：本题考查了正方体相对面上的文字，设相对面上的两个数的和等于k，然后用k表示出x、y、z是解题的关键．
练习册系列答案
全能测控期末小状元系列答案
相关题目
2、如图，是一个正方体的表面展开图，正方体的每个面都标注了字母．在展开前，与标注字母a的面相对的面内标注的字母为（ ）
（2012•宜昌模拟）如图是一个正方体的表面展开图，正方体的每个面都标注了数字，展开之前与标有数字3的面相对的一面所标注的数字为（ ）
如图是一个正方体的表面展开图，正方体的每个面都标注了数字，展开之前与标有数字3的面相对的一面所标注的数字为
