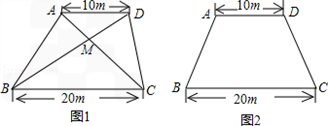
题目内容
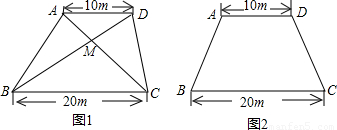
某生活小区的居民筹集资金1600元,计划在一块上、下底分别为10m,20m的梯形空地上种植花木(如图1)(1)他们在△AMD和△BMC地带上种植太阳花,单价为8元/m2,当△AMD地带种满花后(图1中阴影部分),共花了160元,请计算种满△BMC地带所需的费用;
(2)若其余地带要种的有玫瑰和茉莉花两种花木可供选择,单价分别为12元/m2和10元/m2,应选择哪种花木,刚好用完所筹集的资金;
(3)若梯形ABCD为等腰梯形,面积不变(如图2),请你设计一种花坛图案,即在梯形内
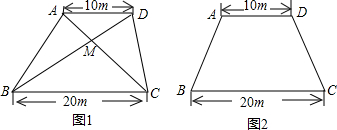 找到一点P,使得△APB≌△DPC且S△APD=S△BPC,并说出你的理由.
找到一点P,使得△APB≌△DPC且S△APD=S△BPC,并说出你的理由.
分析:(1)由太阳花的单价和钱数可先求出△AMD的面积,再由AD∥BC证出△AMD∽△CMB,根据相似三角形面积之比等于相似比的平方,得出△BMC的面积,从而算出所要花费的钱数;
(2)由△AMD∽△CMB,根据相似三角形对应高的比等于它们的相似比,可求出两三角形AD与BC边上的高之比,再根据三角形的面积公式可求出AD边上的高,从而可求出整个梯形的高及面积.进而求出三角形AMB和三角形DCM的面积和,然后根据两种花的单价来计算哪种花合算;
(3)由(2)可知整个梯形高为12,要保证△APB≌△DPC且S△APD=S△BPC,P点必须在AD和BC的垂直平分线上,且P到AD的距离是P到BC距离的2倍,即到AD的距离应该为8.
(2)由△AMD∽△CMB,根据相似三角形对应高的比等于它们的相似比,可求出两三角形AD与BC边上的高之比,再根据三角形的面积公式可求出AD边上的高,从而可求出整个梯形的高及面积.进而求出三角形AMB和三角形DCM的面积和,然后根据两种花的单价来计算哪种花合算;
(3)由(2)可知整个梯形高为12,要保证△APB≌△DPC且S△APD=S△BPC,P点必须在AD和BC的垂直平分线上,且P到AD的距离是P到BC距离的2倍,即到AD的距离应该为8.
解答:解:(1)∵四边形ABCD是梯形,
∴AD∥BC,
∴∠MAD=∠MCB,∠MDA=∠MBC,
∴△AMD∽△CMB,
∴
=(
)2=
.
∵种植△AMD地带花费160元,单价为8元/m2,
∴S三角形AMD=20(m2),
∴S三角形CMB=80m2,
∴△BMC地带所需的费用为8×80=640(元);
(2)设△AMD的高为h1,△BMC的高为h2,梯形ABCD的高为h.
∵S△AMD=
×10h1=20,
∴h1=4,
∵S△BCM=
×20h2=80,
∴h2=8,
∴S梯形ABCD=
(AD+BC)•h
=
×(10+20)×(4+8)
=180.
∴S△AMB+S△DMC=180-20-80=80(m2),
∵160+640+80×12=1760(元),
160+640+80×10=1600(元),
∴应种植茉莉花刚好用完所筹集的资金;
(3)由(2)知梯形高为12,要保证△APB≌△DPC且S△APD=S△BPCP点必须在AD和BC的垂直平分线上,且P到AD的距离是P到BC距离的2倍,即到AD的距离应该为8.
∴AD∥BC,
∴∠MAD=∠MCB,∠MDA=∠MBC,
∴△AMD∽△CMB,
∴
| S三角形AMD |
| S三角形CMB |
| AD |
| BC |
| 1 |
| 4 |
∵种植△AMD地带花费160元,单价为8元/m2,
∴S三角形AMD=20(m2),
∴S三角形CMB=80m2,
∴△BMC地带所需的费用为8×80=640(元);
(2)设△AMD的高为h1,△BMC的高为h2,梯形ABCD的高为h.
∵S△AMD=
| 1 |
| 2 |
∴h1=4,
∵S△BCM=
| 1 |
| 2 |
∴h2=8,
∴S梯形ABCD=
| 1 |
| 2 |
=
| 1 |
| 2 |
=180.
∴S△AMB+S△DMC=180-20-80=80(m2),
∵160+640+80×12=1760(元),
160+640+80×10=1600(元),
∴应种植茉莉花刚好用完所筹集的资金;
(3)由(2)知梯形高为12,要保证△APB≌△DPC且S△APD=S△BPCP点必须在AD和BC的垂直平分线上,且P到AD的距离是P到BC距离的2倍,即到AD的距离应该为8.
点评:此题主要考查了相似三角形的性质以及应用.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
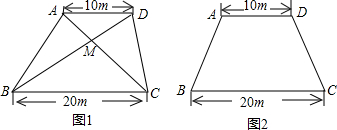 找到一点P,使得△APB≌△DPC且S△APD=S△BPC,并说出你的理由.
找到一点P,使得△APB≌△DPC且S△APD=S△BPC,并说出你的理由.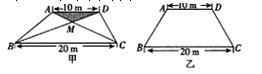
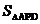 =
=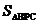 ,并说明理由.
,并说明理由.