题目内容
【题目】如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上,建立平面直角坐标系,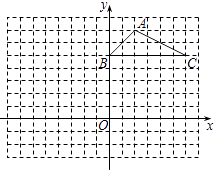
(1)点A的坐标为 , 点C的坐标为 .
(2)将△ABC先向左平移3个单位长度,再向下平移6个单位长度,请画出平移后的△A1B1C1 .
(3)连接A1B,A1C,求△A1BC的面积.
【答案】
(1)(2,7),(6,5)
(2)解:如图所示:△A1B1C1,即为所求;

(3)解:△A1BC的面积为: ![]() ×6×4=12.
×6×4=12.
【解析】解:(1)如图所示:A(2,7),C(6,5);
(2)如图所示:△A1B1C1,即为所求;

(3)△A1BC的面积为: ![]() ×6×4=12.
×6×4=12.
故答案为:(1)(2,7),(6,5);(2)见解答过程;(3)12.
(1)依据点的坐标的定义进行判断即可;
(2)根据平移的方向和距离,确定出各对应点的位置即可;
(3)依据图形,确定出三角形的底边长和高长,最后,再依据三角形的面积公式求解即可.

练习册系列答案
相关题目
【题目】兰州市某中学对本校初中学生完成家庭作业的时间做了总量控制,规定每天完成家庭作业的时间不超过1.5小时,该校数学课外兴趣小组对本校初中学生回家完成作业的时间做了一次随机抽样调查,并绘制出频数分布表和频数分布直方图(如图)的一部分.
时间(小时) | 频数(人数) | 频率 |
0≤t<0.5 | 4 | 0.1 |
0.5≤t<1 | a | 0.3 |
1≤t<1.5 | 10 | 0.25 |
1.5≤t<2 | 8 | b |
2≤t<2.5 | 6 | 0.15 |
合计 | 1 |

(1)在图表中,a= , b=;
(2)补全频数分布直方图;
(3)请估计该校1400名初中学生中,约有多少学生在1.5小时以内完成了家庭作业.
