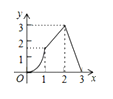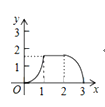题目内容
【题目】平面直角坐标系中,A(a,0),B(0,b),a,b满足![]() ,将线段AB平移得到CD,A,B的对应点分别为C,D,其中点C在y轴负半轴上.
,将线段AB平移得到CD,A,B的对应点分别为C,D,其中点C在y轴负半轴上.
(1)求A,B两点的坐标;
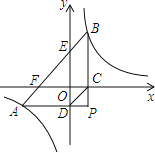
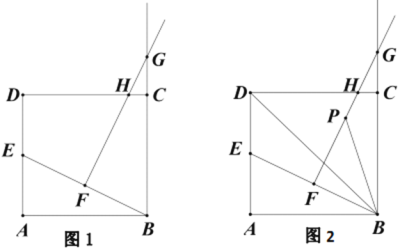
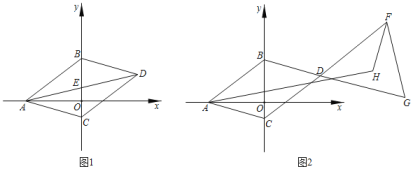
(2)如图1,连AD交BC于点E,若点E在y轴正半轴上,求![]() 的值;
的值;
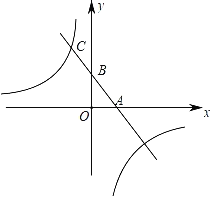
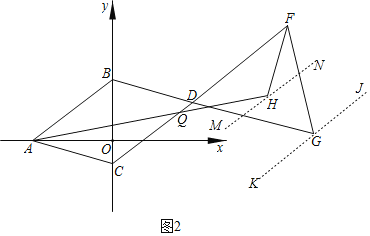
(3)如图2,点F,G分别在CD,BD的延长线上,连结FG,∠BAC的角平分线与∠DFG的角平分线交于点H,求∠G与∠H之间的数量关系.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 与
与![]() 之间的数量关系为
之间的数量关系为![]() .
.
【解析】
(1)根据非负数的性质和解二元一次方程组求解即可;
(2)设![]() ,先根据平移的性质可得
,先根据平移的性质可得![]() ,过D作
,过D作![]() 轴于P,再根据三角形ADP的面积得出
轴于P,再根据三角形ADP的面积得出![]() ,从而可得
,从而可得![]() ,然后根据线段的和差可得
,然后根据线段的和差可得![]() ,由此即可得出答案;
,由此即可得出答案;
(3)设AH与CD交于点Q,过H,G分别作DF的平行线MN,KJ,设![]() ,由平行线的性质可得
,由平行线的性质可得![]() ,由此即可得出结论.
,由此即可得出结论.
(1)∵![]() ,且
,且![]()
∴![]()
解得:![]()
则![]() ;
;
(2)设![]()
∵将线段AB平移得到CD,![]()
∴由平移的性质得![]()
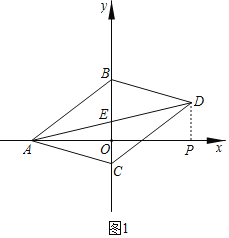
如图1,过D作![]() 轴于P
轴于P
∴![]()
∵![]()
∴![]()
即![]()
解得![]()
∴![]()
∴![]() ;
;
(3)![]() 与
与![]() 之间的数量关系为
之间的数量关系为![]() ,求解过程如下:
,求解过程如下:
如图2,设AH与CD交于点Q,过H,G分别作DF的平行线MN,KJ
∵HD平分![]() ,HF平分
,HF平分![]()
∴设![]()
∵AB平移得到CD
∴![]()
∴![]() ,
,![]()
∴![]()
∵![]()
∴![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴![]() .
.

练习册系列答案
相关题目