题目内容
 已知:如图,圆内接四边形ABCD,过C点作对角线BD的平行线交AD的延长线于E点.
已知:如图,圆内接四边形ABCD,过C点作对角线BD的平行线交AD的延长线于E点.
求证:DE•AB=BC•CD.
 证明:连接AC,
证明:连接AC,则∠BAC=∠BDC,
∵CE∥BD,
∴∠DCE=∠BDC,
∴∠DCE=∠BAC,
∵ABCD是圆内接四边形,
∴∠CDE=∠ABC,
∴△CDE∽△ABC,
∴
 ,
,即DE•AB=BC•CD.
分析:欲证DE•AB=BC•CD,需证△CDE∽△ABC,根据圆周角定理可证∠BAC=∠BDC,又由CE∥BD,可证∠DCE=∠BDC,即证∠DCE=∠BAC,又根据圆内接四边形的性质可证∠CDE=∠ABC,故△CDE∽△ABC得证.
点评:本题考查了相似三角形的判定和性质,圆内接四边形的性质等知识点.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目

 ,
,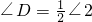 .∵∠1+∠2=360°∴
.∵∠1+∠2=360°∴ ,同理∠BAD+∠BCD=180°,即圆内接四边形对角(相对的两个角)互补.
,同理∠BAD+∠BCD=180°,即圆内接四边形对角(相对的两个角)互补.