题目内容
某化工材料经销公司购进了一种化工原料共7000千克，购进价格为每千克30元．物价部门规定其销售价格不得高于每千克70元，也不得低于30元，市场调查发现：单价定为70元时，日均销售60千克；单价每降低1元，日均多售出2千克．在销售过程中，每天还要支出其他费用500元（天数不足一天时，按一天计算），设销售单价为x元，日均获利y元．
（1）求y关于x的二次函数关系时，并注明x的取值范围；
（2）将（1）中所求的二次函数关系式配方成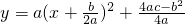
形式，写出顶点坐标，在坐标系中画出草图；观察图象指出单价定为多少元时日均获利最多，是多少？
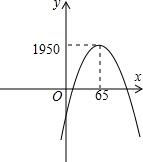解：（1）y=（x-30）（60+2（70-x））-500=-2x2+260x-6500（30≤x≤70）；
（2）y=-2（x-65）2+1950，顶点是（65，1950），单价定为65元时，日均获利最多是1950元．
分析：（1）日利润=每千克的利润×日销售量-杂支，根据物价部门规定，x的取值范围是30≤x≤70；
（2）用配方法变形，根据对称性画草图解答．
点评：认真审题，正确表示利润是关键；运用配方法变形是求最值时常用的手段，应熟练掌握．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
