题目内容
阅读材料题
对于题目“若方程
=-1的解是正数,求a的取值范围.”有同学作了如下解答:
解:去分母,得 2x+a=-x+2
化简,得3x=2-a
所以 x=
欲使方程的解为正数,必须
>0,得a<2
所以当a<2时,方程
=-1的解是正数.
上述解法是否有误?若有错误,请指出错误原因,并写出正确解法;
若无错误,请说明每一步变形的依据.
对于题目“若方程
| 2x+a |
| x-2 |
解:去分母,得 2x+a=-x+2
化简,得3x=2-a
所以 x=
| 2-a |
| 3 |
| 2-a |
| 3 |
所以当a<2时,方程
| 2x+a |
| x-2 |
上述解法是否有误?若有错误,请指出错误原因,并写出正确解法;
若无错误,请说明每一步变形的依据.
分析:化为整式方程,求得x的值然后根据解的情况进行分析没有错,但还应考虑分母x-2≠0即x≠2.
解答:解:该同学解法有误.原因:
当a<2时,分母有可能为零,即
=2,则方程无解.
正确解法:
第四步后:欲使方程的解为正数,必须
>0且
≠2.
得a<2且a≠-4.所以当a<2且a≠-4时,方程
=-1的解是正数.
当a<2时,分母有可能为零,即
| 2-a |
| 3 |
正确解法:
第四步后:欲使方程的解为正数,必须
| 2-a |
| 3 |
| 2-a |
| 3 |
得a<2且a≠-4.所以当a<2且a≠-4时,方程
| 2x+a |
| x-2 |
点评:本题考查了分式方程的解.需注意在任何时候都要考虑分母不为0的情况.

练习册系列答案
相关题目
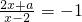 的解是正数,求a的取值范围.”有同学作了如下解答:
的解是正数,求a的取值范围.”有同学作了如下解答: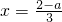 欲使方程的解为正数,必须
欲使方程的解为正数,必须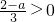 ,得a<2
,得a<2