题目内容
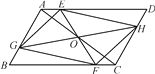
【题目】如图，ABCD 中，点O 是对角线AC 的中点，EF 过点O，与AD，BC 分别相交于点E，F，GH 过点O，与AB，CD 分别相交于点G，H，连接EG，FG，FH，EH.求证：四边形EGFH 是平行四边形．
【答案】证明见解析.
【解析】试题分析: 由四边形ABCD是平行四边形，得到AD∥BC，根据平行四边形的性质得到∠EAO=∠FCO，证出△OAE≌△OCF，得到OE=OF，同理OG=OH，根据对角线互相平分的四边形是平行四边形得到结论．
试题解析:
∵四边形ABCD 为平行四边形，
∴AD∥BC.
∴∠EAO＝∠FCO.
∵O为AC的中点，
∴OA＝OC.
在△OAE和△OCF中，
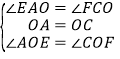
∴△OAE≌△OCF(ASA)．
∴OE＝OF.
同理可证得OG＝OH.
∴四边形EGFH是平行四边形．
点睛: 此题主要考查了平行四边形的性质与判定，关键是掌握平行四边形对角线互相平分，对角线互相平分的四边形是平行四边形．
练习册系列答案
阅读快车系列答案
相关题目
