��Ŀ����
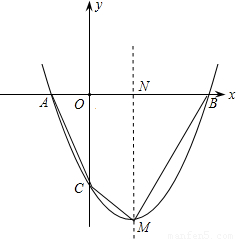
��2002•���ݣ���֪��������y=ax2+bx+c��y�ύ�ڵ�C����x�ύ�ڵ�A��x1��0����b��x2��0����x1��x2��������M����������-4����x1��x2�Ƿ���x2-2��m-1��+m2-7=0������ʵ��������x12+x22=10����1����A��B��������ꣻ
��2���������ߵĽ���ʽ��
��3�������������Ƿ���ڵ�P��ʹ��PAB����������ı���ACMB�������2���������ڣ�������к������ĵ�P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���������1������Τ�ﶨ���ɵó�A��B���������ĺ����������x12+x22=10�������m��ֵ�����������A��B�����꣮
��2������A��B�����꣬�ɵó������ߵĶԳ���Ľ���ʽ����������䶥��M�����꣬���ݵó���A��B��M��������꣬�����ô���ϵ������������ߵĽ���ʽ��
��3����������ı���ACMB������������ı���ACMB�����������������÷ָ������⣩��Ȼ�����ACMB�������P���������ľ���ֵ��������������ߵĽ���ʽ�м������P������꣮
��� �⣺��1������x1��x2�Ƿ���x2-2��m-1��+m2-7=0������ʵ������
�⣺��1������x1��x2�Ƿ���x2-2��m-1��+m2-7=0������ʵ������
������ã�x1+x2�T-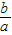 =2��m-1����x1x2=
=2��m-1����x1x2=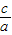 =m2-7��
=m2-7��
��x12+x22=��x1+x2��2-2x1x2=4��m-1��2-2��m2-7��=10��
����m2-4m+4=0��
���m=2��
�ҵ�m=2ʱ����=4-4×��-3����0���������⣮
��ԭ���̿�д�ɣ�x2-2x-3=0��
��x1��x2��
��x1=-1��x2=3��
��A��-1��0����B��3��0����
��2����֪��A��-1��0����B��3��0����
�������ߵĶԳ���Ϊx=1��
��������ߵĶ�������Ϊ��1��-4����
�������ߵĽ���ʽΪy=a��x+1����x-3�������У�
-4=a��1+1����1-3����a=1��
��y=��x-3����x+1��=x2-2x-3��
��3��S�ı���ACMB=S��AOC+S����OCMN+S��NBM= OA•OC+
OA•OC+ ��OC+MN��•ON+
��OC+MN��•ON+ NB•MN��
NB•MN��
= ×1×3+
×1×3+ ×��3+4��×1+
×��3+4��×1+ ×2×4=9��
×2×4=9��
�������P��x��y��ʹ��S��PAB=2S�ı���ACMB=18��
���� AB|y|=18��
AB|y|=18�� ×4×|y|=18��
×4×|y|=18��
��y=±9��
��y=9ʱ��x2-2x-3=9�����x=1-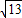 ��x=1+
��x=1+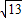 ��
��
��y=-9ʱ��x2-2x-3=-9���˷�����ʵ������
����ڷ���������P�㣬������Ϊ��1-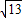 ��9������1+
��9������1+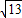 ��9����
��9����
��������Ҫ����һԪ���η��̸���ϵ���Ĺ�ϵ�����κ�������ʽ��ȷ����ͼ�ε������֪ʶ���ۺ�Ӧ��֪ʶ����������������
��2������A��B�����꣬�ɵó������ߵĶԳ���Ľ���ʽ����������䶥��M�����꣬���ݵó���A��B��M��������꣬�����ô���ϵ������������ߵĽ���ʽ��
��3����������ı���ACMB������������ı���ACMB�����������������÷ָ������⣩��Ȼ�����ACMB�������P���������ľ���ֵ��������������ߵĽ���ʽ�м������P������꣮
���
 �⣺��1������x1��x2�Ƿ���x2-2��m-1��+m2-7=0������ʵ������
�⣺��1������x1��x2�Ƿ���x2-2��m-1��+m2-7=0������ʵ������������ã�x1+x2�T-
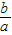 =2��m-1����x1x2=
=2��m-1����x1x2=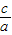 =m2-7��
=m2-7����x12+x22=��x1+x2��2-2x1x2=4��m-1��2-2��m2-7��=10��
����m2-4m+4=0��
���m=2��
�ҵ�m=2ʱ����=4-4×��-3����0���������⣮
��ԭ���̿�д�ɣ�x2-2x-3=0��
��x1��x2��
��x1=-1��x2=3��
��A��-1��0����B��3��0����
��2����֪��A��-1��0����B��3��0����
�������ߵĶԳ���Ϊx=1��
��������ߵĶ�������Ϊ��1��-4����
�������ߵĽ���ʽΪy=a��x+1����x-3�������У�
-4=a��1+1����1-3����a=1��
��y=��x-3����x+1��=x2-2x-3��
��3��S�ı���ACMB=S��AOC+S����OCMN+S��NBM=
 OA•OC+
OA•OC+ ��OC+MN��•ON+
��OC+MN��•ON+ NB•MN��
NB•MN��=
 ×1×3+
×1×3+ ×��3+4��×1+
×��3+4��×1+ ×2×4=9��
×2×4=9���������P��x��y��ʹ��S��PAB=2S�ı���ACMB=18��
����
 AB|y|=18��
AB|y|=18�� ×4×|y|=18��
×4×|y|=18����y=±9��
��y=9ʱ��x2-2x-3=9�����x=1-
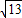 ��x=1+
��x=1+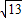 ��
����y=-9ʱ��x2-2x-3=-9���˷�����ʵ������
����ڷ���������P�㣬������Ϊ��1-
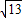 ��9������1+
��9������1+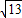 ��9����
��9������������Ҫ����һԪ���η��̸���ϵ���Ĺ�ϵ�����κ�������ʽ��ȷ����ͼ�ε������֪ʶ���ۺ�Ӧ��֪ʶ����������������

��ϰ��ϵ�д�
 ��У��ʦ������ҵ���Ӻ����Ծ�ϵ�д�
��У��ʦ������ҵ���Ӻ����Ծ�ϵ�д� ȫ�̽��ϵ�д�
ȫ�̽��ϵ�д�
�����Ŀ