题目内容
附加题:已知Rt△ABC中,∠ACB=90°,AC=6,BC=8.
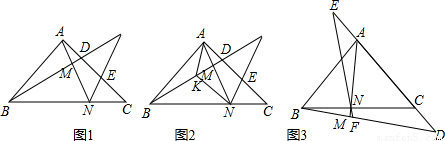
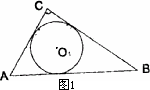
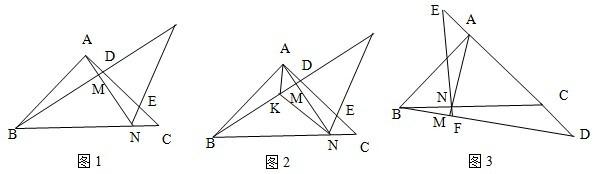
(1)如图1,若半径为r1的⊙O1是Rt△ABC的内切圆,求r1;
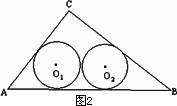
(2)如图2,若半径为r2的两个等圆⊙O1、⊙O2外切,且⊙O1与AC、AB相切,⊙O2与BC、AB相切,求r2;
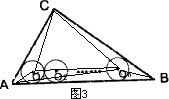
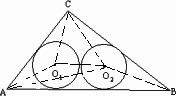
(3)如图3,当n是大于2的正整数时,若半径为rn的n个等圆⊙O1、⊙O2、……、⊙ON依次外切,且⊙O1与AC、AB相切,⊙On与BC、AB相切,⊙O2、⊙O3、……、⊙On-1均与AB边相切,求rn.
答案:
解析:
解析:
|
(1)解:设⊙ ∵ ∴∠1=∠2= ∴∠1=∠2=∠ACB= ∴四边形CF ∴ ∵⊙O为Rt△ABC内切圆 ∴CF=CE BE=BD AD=AF ∵∠ACB= ∴△ACB为Rt△ ∴ ∴AB=10(舍负) ∴AF=AD=6- BD=BE=8- ∴AB=6 ∴⊙ (2)解:连结
(3)解:
|

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
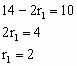
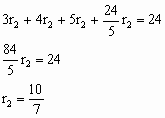
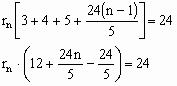
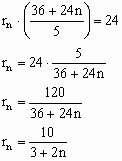
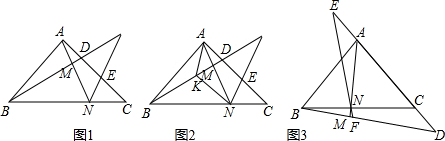 状,并说明理由.
状,并说明理由.