题目内容
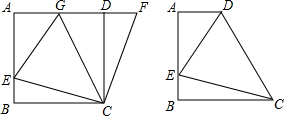 (2009•沈阳模拟)如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
(2009•沈阳模拟)如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.(1)求证:CE=CF;
(2)在图1中,若G在AD上,且∠GCE=45°,探索GE、BE、GD之间的数量关系,并加以证明;
(3)运用(1)、(2)解答中所积累的经验和知识,完成下题:
如图2,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC=10,E是AB上一点,且∠DCE=45°,BE=3,求DE的长.
分析:(1)由条件直接证明三角形全等就可以得出CE=CF.
(2)由条件和(1)的结论可以证明三角形ECG全等三角形FCG,可以得出EG=FG,可以得出GE=BE+GD.
(3)过点C作CD⊥AD交AG的延长线于点D,延长AG使DH=BE,从而运用(2)的结论可以表示出DG,由勾股定理就可以求出DE的值.
(2)由条件和(1)的结论可以证明三角形ECG全等三角形FCG,可以得出EG=FG,可以得出GE=BE+GD.
(3)过点C作CD⊥AD交AG的延长线于点D,延长AG使DH=BE,从而运用(2)的结论可以表示出DG,由勾股定理就可以求出DE的值.
解答:解:(1)证明:在正方形ABCD中,
∴AB=BC=CD=AD,∠A=∠B=∠BCD=∠ADC.
∵BC=CD,∠B=∠CDF,BE=DF,
∴△CBE≌△CDF(SAS),
∴CE=CF.
(2)GE=BE+GD
∵△CBE≌△CDF,
∴∠BCE=∠DCF.
∵∠GCE=45°,
∴∠BCE+∠GCD=45°
∴∠GCD+∠DCF=∠GCF=45°,
∴∠GCF=∠GCE,
∴△GCE≌△GCF,
∴GE=GF,
∵GF=GD+DF,
∴GE=GD+DF,
∴GE=GD+BE.
(3))过点C作CD⊥AD交AG的延长线于点D,延长AG使DH=BE,连结CH.
在直角梯形ABCD中,
∵AD∥BC,∠A=∠B=90°,∠ADC=90°,AB=BC,
∴四边形ABCD是正方形.
∵∠DCE=45°,由(2)的结论,得
GE=DG+BE,设DE=x,则DG=x-3,
∴AD=13-x.
在Rt△AED中
DE2=AD2+AE2,
x2=(13-x)2+72,
解得:x=
∴DE=
.

∴AB=BC=CD=AD,∠A=∠B=∠BCD=∠ADC.
∵BC=CD,∠B=∠CDF,BE=DF,
∴△CBE≌△CDF(SAS),
∴CE=CF.
(2)GE=BE+GD
∵△CBE≌△CDF,
∴∠BCE=∠DCF.
∵∠GCE=45°,
∴∠BCE+∠GCD=45°
∴∠GCD+∠DCF=∠GCF=45°,
∴∠GCF=∠GCE,
∴△GCE≌△GCF,
∴GE=GF,
∵GF=GD+DF,
∴GE=GD+DF,
∴GE=GD+BE.
(3))过点C作CD⊥AD交AG的延长线于点D,延长AG使DH=BE,连结CH.
在直角梯形ABCD中,
∵AD∥BC,∠A=∠B=90°,∠ADC=90°,AB=BC,
∴四边形ABCD是正方形.
∵∠DCE=45°,由(2)的结论,得
GE=DG+BE,设DE=x,则DG=x-3,
∴AD=13-x.
在Rt△AED中
DE2=AD2+AE2,
x2=(13-x)2+72,
解得:x=
| 109 |
| 13 |
∴DE=
| 109 |
| 13 |

点评:本题考查了正方形的性质和全等三角形的判定与性质,勾股定理的运用及直角梯形的性质,学生熟练掌握这些性质定理是正确解答的基础.

练习册系列答案
相关题目
 求解)
求解)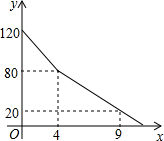 手中持有的钱数y(元)与购买糖果的数量x(千克)之间的函数关系如下图所示,请结合图象,回答下列问题:
手中持有的钱数y(元)与购买糖果的数量x(千克)之间的函数关系如下图所示,请结合图象,回答下列问题: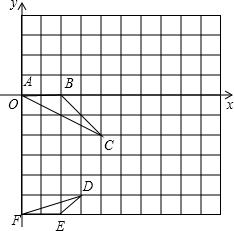 形顶点上,且点A与原点重合.
形顶点上,且点A与原点重合.