题目内容
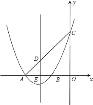
【题目】如图,已知抛物线y=x2+4x+3交x轴于A、B两点,交y轴于点C,抛物线的对称轴交x轴于点E,点B的坐标为(﹣1,0).
(1)求抛物线的对称轴及点A的坐标;
(2)在平面直角坐标系xoy中是否存在点P,与A、B、C三点构成一个平行四边形?若存在,请写出点P的坐标;若不存在,请说明理由;
(3)连接CA与抛物线的对称轴交于点D,在抛物线上是否存在点M,使得直线CM把四边形DEOC分成面积相等的两部分?若存在,请求出直线CM的解析式;若不存在,请说明理由.
【答案】(1)对称轴x=﹣![]() =﹣2;点A的坐标为(﹣3,0)
=﹣2;点A的坐标为(﹣3,0)
(2)满足条件的点P有3个,分别为(﹣2,3),(2,3),(﹣4,﹣3);
(3)存在;直线CM的解析式为y=![]() x+3.
x+3.
【解析】
试题分析:(1)根据二次函数y=ax2+bx+c的对称轴为x=﹣![]() ,求得抛物线的对称轴,因为函数与X轴的交点是y=0,列方程即可求得;
,求得抛物线的对称轴,因为函数与X轴的交点是y=0,列方程即可求得;
(2)分别以AC,AB为对角线各可求得一点,再以AC,AB为边求得一点;
(3)首先可求得梯形DEOC的面积,根据题意:在OE上找点F,使OF=![]() ,此时S△COF=
,此时S△COF=![]() ×
×![]() ×3=2,直线CF把四边形DEOC分成面积相等的两部分,交抛物线于点M,设直线CM的解析式为y=kx+3,它经过点F(﹣
×3=2,直线CF把四边形DEOC分成面积相等的两部分,交抛物线于点M,设直线CM的解析式为y=kx+3,它经过点F(﹣![]() ,0),则﹣
,0),则﹣![]() k+3=0,解之,得k=
k+3=0,解之,得k=![]() .∴直线CM的解析式为y=
.∴直线CM的解析式为y=![]() x+3.
x+3.
试题解析:(1)①对称轴x=﹣![]() =﹣2;
=﹣2;
②当y=0时,有x2+4x+3=0,解之,得x1=﹣1,x2=﹣3,∴点A的坐标为(﹣3,0).
(2)满足条件的点P有3个,分别为(﹣2,3),(2,3),(﹣4,﹣3).
(3)存在.
当x=0时,y=x2+4x+3=3,∴点C的坐标为(0,3),∵DE∥y轴,AO=3,EO=2,AE=1,CO=3,
∴△AED∽△AOC,∴![]() 即
即![]() ,∴DE=1.∴S梯形DEOC=
,∴DE=1.∴S梯形DEOC=![]() (1+3)×2=4,
(1+3)×2=4,
在OE上找点F,使OF=![]() ,此时S△COF=
,此时S△COF=![]() ×
×![]() ×3=2,直线CF把四边形DEOC分成面积相等的两部分,交抛物线于点M.设直线CM的解析式为y=kx+3,它经过点F(﹣
×3=2,直线CF把四边形DEOC分成面积相等的两部分,交抛物线于点M.设直线CM的解析式为y=kx+3,它经过点F(﹣![]() ,0).
,0).
则﹣![]() k+3=0,解之,得k=
k+3=0,解之,得k=![]() ,∴直线CM的解析式为y=
,∴直线CM的解析式为y=![]() x+3.
x+3.

 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案