Question

四个半径均为r的圆如图放置，相邻两圆交点之间的距离也等于r，不相邻两圆圆周上两点间的最短距离等于2，则r等于

 

，图中阴影部分面积等于

 

．（精确到0.01）

Answer 1

分析：根据相交两圆的连心线垂直平分两圆的公共弦，进而可得四个圆心组成的图形是正方形，则有

2

×

3

r=2r+2，r=

6

+2；进而可得阴影部分的面积即正方形的面积减去一个圆的面积再加上两个相邻圆的公共部分的面积，计算可得答案．

解答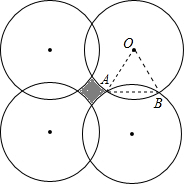：解：根据相交两圆的连心线垂直平分两圆的公共弦．
得相邻两圆的圆心距是

3

r，
根据题意，得四个圆心组成的图形是正方形，
则有

2

×

3

r=2r+2，r=

6

+2；
∵相邻两圆交点之间的距离也等于r，
∴△OAB是等边三角形，
∴两个相邻圆的公共部分的面积为：
2（S_扇形OAB-S_△OAB）=

8+4 6

3

π-4

3

-6

2

，
阴影部分的面积即正方形的面积减去一个圆的面积再加上两个相邻圆的公共部分的面积，即约为4.37；
故答案为

6

+2，4.37．

点评：熟悉相交两圆的性质以及正方形的性质．