Question

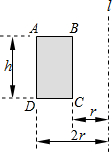已知柱体的体积V=S•h，其中S表示柱体的底面面积，h表示柱体的高．现将矩形ABCD绕轴l旋转一周，则形成的几何体的体积等于

1. A.
   πr²h
2. B.
   2πr²h
3. C.
   3πr²h
4. D.
   4πr²h

Answer 1

C
分析：根据柱体的体积V=S•h，求出形成的几何体的底面积，即可得出体积．
解答：∵柱体的体积V=S•h，其中S表示柱体的底面面积，h表示柱体的高，现将矩形ABCD绕轴l旋转一周，
∴柱体的底面圆环面积为：π（2r）²-πr²=3πr²，
∴形成的几何体的体积等于：3πr²h．
故选：C．
点评：此题主要考查了圆柱体体积公式，根据已知得出柱体的底面面积是解决问题的关键．