题目内容
如图，若正方形AB′C′D′是由边长为2的正方形ABCD绕点A按逆时针方向旋转30°而成的，则DB′的长度为2
2
．分析：根据旋转的性质得出AB=AB′=AD，∠DAB′=60°，进而得出△ADB′是等边三角形，即可得出DB′的长度．
解答：解：∵正方形AB′C′D′是由边长为2的正方形ABCD绕点A按逆时针方向旋转30°而成的，
∴∠BAB′=30°，AB=AB′=AD，
∴∠DAB′=60°，
∴△ADB′是等边三角形，
∴DB′=AD=2．
故答案为：2．
∴∠BAB′=30°，AB=AB′=AD，
∴∠DAB′=60°，
∴△ADB′是等边三角形，
∴DB′=AD=2．
故答案为：2．
点评：此题主要考查了旋转的性质以及等边三角形的判定与性质，得出∠DAB′=60°是解题关键．
练习册系列答案
愉快的寒假南京出版社系列答案
相关题目
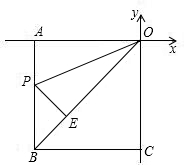如图，若正方形ABCO的各顶点的坐标为A（-2，0），B（-2，-2），C（0，-2），O（0，0），把正方形沿OP对折，使点A落在对角线OB上的E处，折痕交AB于E，试求△EPO的面积．
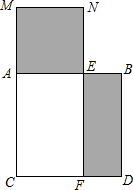已知线段AB的长为2，以AB为边在AB的下方作正方形ACDB．取AB边上一点E，以AE为边在AB的上方作正方形AENM．过E作EF⊥CD，垂足为F点，如图．若正方形AENM与四边形EFDB的面积相等，則AE的长为
（2012•宁德质检）如图，若正方形ABCD的面积为57，则边AB的长介于连续整数