题目内容
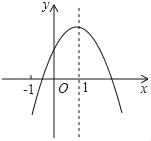
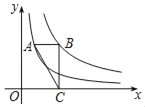
【题目】如图1,抛物线y=ax2+bx+c的图象与x轴交于A(﹣3,0)、B(1,0)两点,与y轴交于点C,且OC=OA.
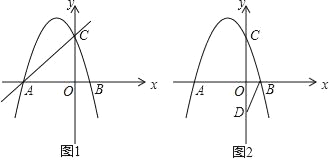
(1)求抛物线解析式;
(2)过直线AC上方的抛物线上一点M作y轴的平行线,与直线AC交于点N.已知M点的横坐标为m,试用含m的式子表示MN的长及△ACM的面积S,并求当MN的长最大时S的值;
(3)如图2,D(0,﹣2),连接BD,将△OBD绕平面内的某点(记为P)逆时针旋转180°得到△O′B′D′,O、B、D的对应点分别为O′、B′、D′.若点B′、D′两点恰好落在抛物线上,求旋转中心点P的坐标.
【答案】(1)y=﹣x2﹣2x+3;(2)MN=﹣m2﹣3m(﹣3<m<0),S△ACM=![]() ,m=﹣
,m=﹣![]() 时,MN最大,此时S=
时,MN最大,此时S=![]() ;(3)P(-
;(3)P(-![]() ,
,![]() ).
).
【解析】
(1)先求出点A坐标,再运用待定系数法求解即可;
(2)先求出直线AC的解析式,待定点M,N的坐标,用m表示线段MN的长度,运用二次函数分析其最值即可;
(3)根据中心对称的性质,明确B′D′与BD平行且相等,待定点B′、D′的坐标,代入抛物线解析式求解即可得出B′、D′的坐标,而后运用中点公式求出中心的坐标即可;
解:(1)由A(﹣3,0),且OC=OA可得
A(﹣3,0)
设抛物线解析式为y=a(x+3)(x﹣1),
将C(0,3)代入解析式得,﹣3a=3,解得a=﹣1,
∴抛物线解析式为y=﹣x2﹣2x+3.
(2)如图1,
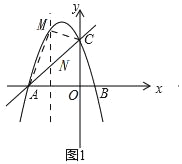
设直线AC解析式为y=kx+d
∵A(﹣3,0),C(0,3),
∴![]() ,
,
解得![]() ,
,
∴直线AC解析式为y=x+3,
设M(m,﹣m2﹣2m+3),则N(m,m+3),则MN=﹣m2﹣2m+3﹣(m+3)=﹣m2﹣3m(﹣3<m<0),
S△ACM=S△AMN+S△CMN=![]() MN×3=
MN×3=![]() ,
,
MN=﹣m2﹣3m=﹣![]() +
+![]() ,
,
∵a=﹣1<0,﹣3<m=﹣1.5<0,
∴m=﹣![]() 时,MN最大,此时S=
时,MN最大,此时S=![]() ;
;
(3)如图2中,旋转180°后,对应线段互相平行且相等,则BD与B′D′互相平行且相等.
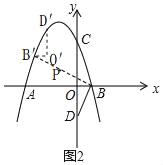
∵O′B′=OB=1,O′D′=OD=2,
设B′(t,﹣t2﹣2t+3),则D′(t+1,﹣t2﹣2t+3+2)
∵D′在抛物线上,则﹣(t+1)2﹣2(t+1)+3=﹣t2﹣2t+3+2,
解得,t=-![]() ,则B′的坐标为(-
,则B′的坐标为(-![]() ,
,![]() ),
),
P是点B(1,0)和点B′(-![]() ,
,![]() ),的对称中心,
),的对称中心,
![]() ,
,![]() ,
,
∴P(-![]() ,
,![]() ).
).