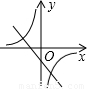
题目内容
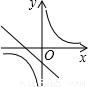
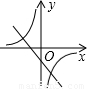
函数y1=ax-a与y2=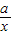 (a≠0)在同一坐标系内的图象大致是( )
(a≠0)在同一坐标系内的图象大致是( )A.

B.

C.
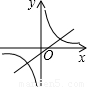
D.

【答案】分析:因为a的符号不确定,所以应根据a的符号及函数图象的特点进行分类讨论.
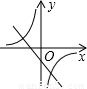
解答:解:当a<0时,-a>0,反比例函数y2= (a≠0)的图象在二,四象限,一次函数y1=ax-a的图象过一,二,四象限,无选项符合;
(a≠0)的图象在二,四象限,一次函数y1=ax-a的图象过一,二,四象限,无选项符合;
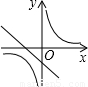
当a>0时,-a<0,反比例函数y2= (a≠0)的图象在一、三象限,一次函数y1=ax-a的图象过一、三、四象,选项C符合.
(a≠0)的图象在一、三象限,一次函数y1=ax-a的图象过一、三、四象,选项C符合.
故选C.
点评:本题主要考查了反比例函数的图象性质和一次函数的图象性质,关键是由a的取值确定函数所在的象限.
解答:解:当a<0时,-a>0,反比例函数y2=
 (a≠0)的图象在二,四象限,一次函数y1=ax-a的图象过一,二,四象限,无选项符合;
(a≠0)的图象在二,四象限,一次函数y1=ax-a的图象过一,二,四象限,无选项符合;当a>0时,-a<0,反比例函数y2=
 (a≠0)的图象在一、三象限,一次函数y1=ax-a的图象过一、三、四象,选项C符合.
(a≠0)的图象在一、三象限,一次函数y1=ax-a的图象过一、三、四象,选项C符合.故选C.
点评:本题主要考查了反比例函数的图象性质和一次函数的图象性质,关键是由a的取值确定函数所在的象限.

练习册系列答案
相关题目
函数y1=ax-a与y2=
(a≠0)在同一坐标系内的图象大致是( )
| a |
| x |
A、 |
B、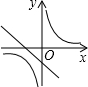 |
C、 |
D、 |
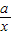 (a≠0)在同一坐标系内的图象大致是( )
(a≠0)在同一坐标系内的图象大致是( )

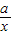 (a≠0)在同一坐标系内的图象大致是( )
(a≠0)在同一坐标系内的图象大致是( )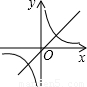

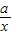 (a≠0)在同一坐标系内的图象大致是( )
(a≠0)在同一坐标系内的图象大致是( )