题目内容
(1998•上海)已知一个二次函数的图象经过A(-1,0)、B(0,3)、C(4,-5)三点.(1)求这个二次函数的解析式及其图象的顶点D的坐标;
(2)这个函数的图象与x轴有两个交点,除点A外的另一个交点设为E,点O为坐标原点.在△AOB、△BOE、△ABE和△BDE着四个三角形中,是否有相似三角形?如果有,指出哪几对三角形相似,并加以证明;如果没有,要说明理由.
【答案】分析:(1)使用代入法可求解二次函数的解析式.
(2)在坐标轴上每一点的坐标都是已知,则可根据两点间的距离公式求得每一线段的长,若在两三角形中,三边对应成比例,而这两三角形相似,可推得△AOB∽△DBE.
解答:解:(1)设二次函数的解析式为y=ax2+bx+c(a≠0).
根据题意,得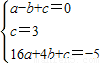 ,
,
解得a=-1,b=2,c=3.
∴二次函数的解析式为y=-x2+2x+3.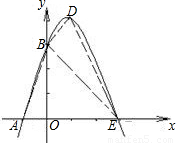
由y=-x2+2x+3=-(x-1)2+4,
得顶点D的坐标为(1,4)
答:顶点D的坐标为(1,4);
(2)在直角坐标平面内画出图形.
△AOB∽△DBE,
∵OA=1,OB=3,AB=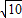 ,BD=
,BD=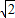 ,BE=3
,BE=3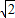 ,DE=
,DE=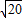 .
.
得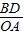 =
=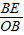 =
=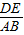 =
=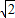 .
.
∴△AOB∽△DBE.
点评:用待定系数法求函数的解析式时要灵活地根据已知条件选择配方法和公式法.本题是一道难度较大的二次函数题,综合考查了三角形相似的判定定理.
(2)在坐标轴上每一点的坐标都是已知,则可根据两点间的距离公式求得每一线段的长,若在两三角形中,三边对应成比例,而这两三角形相似,可推得△AOB∽△DBE.
解答:解:(1)设二次函数的解析式为y=ax2+bx+c(a≠0).
根据题意,得
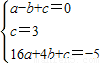 ,
,解得a=-1,b=2,c=3.
∴二次函数的解析式为y=-x2+2x+3.

由y=-x2+2x+3=-(x-1)2+4,
得顶点D的坐标为(1,4)
答:顶点D的坐标为(1,4);
(2)在直角坐标平面内画出图形.
△AOB∽△DBE,
∵OA=1,OB=3,AB=
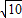 ,BD=
,BD=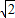 ,BE=3
,BE=3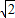 ,DE=
,DE=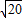 .
.得
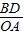 =
=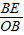 =
=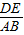 =
=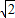 .
.∴△AOB∽△DBE.
点评:用待定系数法求函数的解析式时要灵活地根据已知条件选择配方法和公式法.本题是一道难度较大的二次函数题,综合考查了三角形相似的判定定理.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目