题目内容
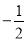 的相反数是( )
的相反数是( )
A.2 B.-2 C. D.
D.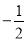
C.
【解析】
试题分析:根据相反数的意义知: 的相反数是
的相反数是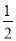 .
.
故选C.
考点:相反数.

练习册系列答案
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
题目内容
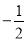 的相反数是( )
的相反数是( )
A.2 B.-2 C. D.
D.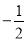
C.
【解析】
试题分析:根据相反数的意义知: 的相反数是
的相反数是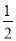 .
.
故选C.
考点:相反数.

 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案