Question

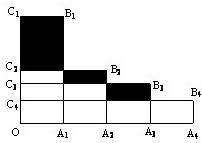12、长方形OA₁B₁C₁，OA₂B₂C₂，OA₃B₃C₃，OA₄B₄C₄的面积都为4cm²，且OA₁=A₁A₂=A₂A₃=A₃A₄，则图中三块阴影部分的面积和为

3

cm²．

Answer 1

分析：认真观察图形，由于OA₁=A₁A₂=A₂A₃=A₃A₄及OA₄B₄C₄的面积为4cm²，可得最下面一行的四个小长方形的面积，每一行的小长方形的面积都是分别相等的，把右边的两个阴影的小长方形平行移到左边，可利用长方形OA₁B₁C₁的面积减去1得到答案．

解答：解：∵OA₁=A₁A₂=A₂A₃=A₃A₄，各小长方形的高相等，
∴每一行的小长方形的面积都是分别相等的，
又OA₄B₄C₄的面积为4cm²，
∴最下面一行的四个小长方形的面积分别为1，
把右边的两个阴影的小长方形平行移到左边，
∴图中三块阴影部分的面积和为：
长方形OA₁B₁C₁的面积-最下边的一个小长方形的面积
=4-1
=3．
故答案为3．

点评：本题考查了面积及等积变换问题；认真观察图形，找出每一行的小长方形的面积都是相等的是正确解答本题的关键．