题目内容
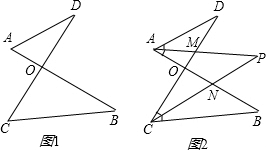
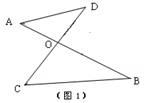
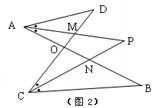
已知如图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.
试解答下列问题:
(1)在图1中,若∠A+∠D=80°,则∠B+∠C=
(2)在图2中,若∠DAO=50°,∠OCB=40°,∠P=35°,试求∠D的度数;
(3)在图2中,若设∠D=x°,∠B=y°,其它条件不变,试求∠P的度数.

试解答下列问题:
(1)在图1中,若∠A+∠D=80°,则∠B+∠C=
80°
80°
;仔细观察,在图2中“8字形”的个数:6
6
个;(2)在图2中,若∠DAO=50°,∠OCB=40°,∠P=35°,试求∠D的度数;
(3)在图2中,若设∠D=x°,∠B=y°,其它条件不变,试求∠P的度数.
分析:(1)根据三角形的内角和定理表示出∠AOD和∠BOC,然后根据对顶角相等列式整理即可得解,然后根据顶点找出“8字形”的个数;
(2)根据角平分线的定义表示出∠1、∠2,再根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠AMO,然后代入数据整理即可得解;
(3)根据三角形的一个外角等于与它不相邻的两个内角的和分别表示出∠AMO和∠ONC,再根据角平分线的定义可得∠1=∠2,∠3=∠4,然后整理即可得解.
(2)根据角平分线的定义表示出∠1、∠2,再根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠AMO,然后代入数据整理即可得解;
(3)根据三角形的一个外角等于与它不相邻的两个内角的和分别表示出∠AMO和∠ONC,再根据角平分线的定义可得∠1=∠2,∠3=∠4,然后整理即可得解.
解答:解:(1)根据三角形的内角和定理,∠AOD=180°-(∠A+∠D)=180°-80°=100°,
∠BOC=180°-(∠B+∠C),
∵∠AOD=∠OC(对顶角相等),
∴∠B+∠C=180°-100°=80°,
如图2,以点O为顶点的“8字形”有△AOD和△BOC,△AOM和△CON,△AOD和△CON,△AOM和△BOC,
以点M为顶点的“8字形”有△ADM和△COP,
以点N为顶点的“8字形”有△ANP和△BCN,
共有4+1+1=6个;
(2)∵AP、CP分别是∠DAO、∠BCO的平分线,
∴∠1=
∠DAO=
×50°=25°,
∠2=
∠OCB=
×40°=20°,
又∵∠AMO=∠1+∠D=∠3+∠P,
∴∠D=∠3+∠P-∠1=20°+35°-25°=30°;
(3)由(2)得,∠AMO=∠1+∠D=∠3+∠P①,
又∠ONC=∠4+∠B=∠2+∠P②,
由①、②得,∠1-∠3=∠P-∠D,
∠2-∠4=∠B-∠P,
由已知得,∠1=∠2,∠3=∠4,
∴∠1-∠3=∠2-∠4,
∴∠P-∠D=∠B-∠P,
∴∠P=
(∠B+∠D)=
(x°+y°).
∠BOC=180°-(∠B+∠C),
∵∠AOD=∠OC(对顶角相等),
∴∠B+∠C=180°-100°=80°,
如图2,以点O为顶点的“8字形”有△AOD和△BOC,△AOM和△CON,△AOD和△CON,△AOM和△BOC,
以点M为顶点的“8字形”有△ADM和△COP,
以点N为顶点的“8字形”有△ANP和△BCN,
共有4+1+1=6个;
(2)∵AP、CP分别是∠DAO、∠BCO的平分线,
∴∠1=
| 1 |
| 2 |
| 1 |
| 2 |
∠2=
| 1 |
| 2 |
| 1 |
| 2 |
又∵∠AMO=∠1+∠D=∠3+∠P,
∴∠D=∠3+∠P-∠1=20°+35°-25°=30°;
(3)由(2)得,∠AMO=∠1+∠D=∠3+∠P①,
又∠ONC=∠4+∠B=∠2+∠P②,
由①、②得,∠1-∠3=∠P-∠D,
∠2-∠4=∠B-∠P,
由已知得,∠1=∠2,∠3=∠4,
∴∠1-∠3=∠2-∠4,
∴∠P-∠D=∠B-∠P,
∴∠P=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了三角形的内角和定理,三角形的一个外角等于与它不相邻的两个内角的和的性质,“8字形”的定义,熟记性质并理解题目信息是解题的关键.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目